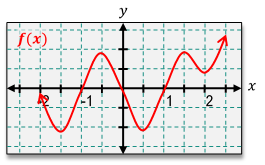
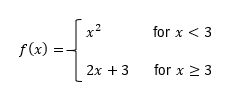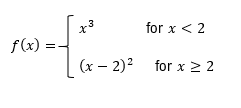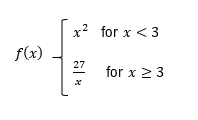So at this point of the course, we should be familiar with the idea of continuity, and recall that a function is continuous if there are no holes, jumps, or asymptotes in your graph, basically meaning you can sketch the whole function without ever having to pick up your pencil. Now in this video, we're going to talk about the idea of differentiability, and a function is differentiable when the derivative exists at all points. This might sound like something that's scary or abstract, but don't sweat it, because it turns out we can combine the idea of finding the derivative of a function based on its graph with the idea of continuity to determine whether or not a function is differentiable. So let's just jump right into an example to see how we can solve these types of problems. Now here, we're asked to determine if our function, f(x), is continuous and differentiable at x equals 2.
The first thing I'm going to do is figure out whether or not this function is continuous, and this is something we should be familiar with. In order for a function to be continuous, this criteria has to be met where the limit from both sides is equivalent to the function evaluated at that point. I can see that this function clearly exists at x equals 2, and I can also see that the limit from both sides is going to have this y-value of 1. Because the limit and the function are both equal to each other at this y-value of 1, then we would say that this criterion is met and therefore, this function is continuous. But now we need to determine whether or not this function is differentiable.
To determine this, there are a couple of rules that we need to follow. In order for a function to be differentiable, it actually has to be continuous. So the criteria that we just checked off have to be met, and we can see that this function is indeed continuous at x equals 2. However, in addition to that, this function also has to be smooth, meaning there cannot be any sharp corners or turns in our graph. By looking at our graph, I can see that there is a sudden corner. There's a sharp turn that happens, which would mean the tangent lines will abruptly change as we go from left to right. And we discussed this when we talked about how to find the graph of a derivative. So because of this, we would say that our derivative does not exist at that point. Therefore, we can conclude that this function is continuous, but it is not differentiable. Based on what we discovered, this would be the solution to our problem.
You may have noticed that this could be a pretty tedious process because there were a lot of boxes that we had to check off with our graph. But recall that there is a shortcut for finding whether or not a function is continuous, and that's if you can sketch the curve without picking up your pencil. Because being continuous is a criterion for differentiability, you also need to make sure you don't have to draw any sharp corners either. In this example, since I had to sketch this curve and suddenly draw this sharp corner down here, it was not differentiable. It is possible for a function to be continuous and not differentiable, but it is not possible for a function to be differentiable but not continuous. With this in mind, let's see if we can solve some more examples using this shortcut.
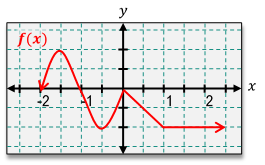
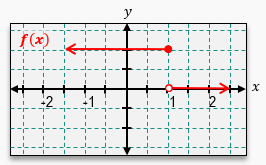
In this example, it says for each interval or x value, determine if the function f(x) is continuous and/or differentiable. The first example here asks us for x equals negative 3, which would be right there. If I try to sketch this graph, notice that all of a sudden if we go from left to right, there's a hole that we run into. So I would have to pick up my pencil here and then put it back down to keep sketching this curve. Because we had to pick up our pencil, we would say this function is not continuous. And by default, if a function is not continuous, then it's not going to be differentiable. But now let's move to example b. Example b asks us to check the point x equals 0. What I can do is I can sketch this from left to right. We'll skip past this point because we already tried it. But if I start right here, well, I can sketch this curve without having to pick up my pencil. So because of that, I would say that this function is continuous. But is it differentiable?
For it to be differentiable, there can't be any sharp corners or turns. If I were to sketch this, notice how I would all of a sudden have a sharp corner right there. And because there's a sharp corner, that means this function is continuous but not differentiable at x equals 0. But now let's take a look at this last piece right here, which asks for this interval, 0 to infinity. So that's going to be this entire portion of the graph right here that just keeps on going. What I can see is that if I were to sketch this portion of the graph, clearly, our function would be continuous because I don't ever have to pick up my pencil no matter how far I sketch this. So we could say that our function is continuous.
But is it differentiable? Well, I can keep sketching this forever and ever, and notice that I would never have a sudden sharp corner or turn. This just keeps on going to the right like this. So because of this, we could say that this function is differentiable. Meaning on this interval, the function is both continuous and differentiable. This is how you can solve these types of problems where you're dealing with differentiability. I hope you found this video helpful, and let's go ahead and get some more practice.