Question to test your Tangent Lines and Derivatives knowledge

Question

An electronic company produces 20,000 tablets per year in batches of x items at a time. The total cost (in $) of the production of 20,000 tablets in batches of x item at a time is given by the function below:
Determine and interpret the meaning of the average and marginal costs when x = 10,000.

Cost function C(x) for tablet production in calculus course.

Determine and interpret the meaning of the average and marginal costs when x = 10,000.

Accepted Answer

Average cost = $126.9

Marginal Cost = −$1.2

When the batch size is 10,000, the average cost of producing 20,000 tablets is $126.9 per tablet. When the batch size is increased by one, the total cost of producing 20,000 tablets will decrease by $1.2.

Answer

Average cost = $126.9

Marginal Cost = $1.2

When the batch size is 10,000, the average cost of producing 10,000 tablets is $126.9 per tablet. When the batch size is increased by one, the total cost of producing 10,000 tablets will increase by $1.2.

Answer

Average cost = $253.8

Marginal Cost = $1.2

When the batch size is 10,000, the average cost of producing 20,000 tablets is $253.8 per tablet. When the batch size is increased by one, the total cost of producing 20,000 tablets will increase by $1.2.

Answer

Average cost = $253.8

Marginal Cost = −$1.2

When the batch size is 10,000, the average cost of producing 10,000 tablets is $253.8 per tablet. When the batch size is increased by one, the total cost of producing 10,000 tablets will decrease by $1.2.

Tangent Lines and Derivatives: Study with Video Lessons, Practice Problems & Examples

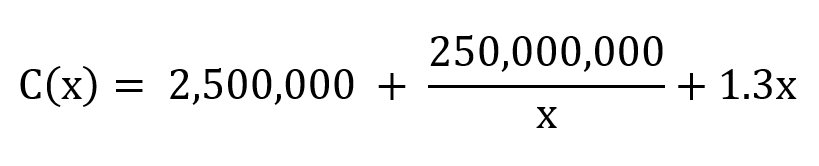
An electronic company produces 20,000 tablets per year in batches of x items at a time. The total cost (in $) of the production of 20,000 tablets in batches of x item at a time is given by the function below:Determine and interpret the meaning of the average and marginal costs when x = 10,000.

An electronic company produces 20,000 tablets per year in batches of x items at a time. The total cost (in $) of the production of 20,000 tablets in batches of x item at a time is given by the function below:
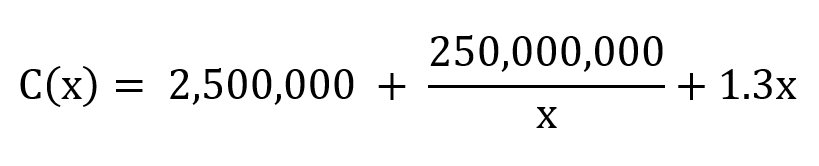
Determine and interpret the meaning of the average and marginal costs when x = 10,000.