Table of contents
- 0. Functions(0)
- Introduction to Functions(0)
- Piecewise Functions(0)
- Properties of Functions(0)
- Common Functions(0)
- Transformations(0)
- Combining Functions(0)
- Exponent rules(0)
- Exponential Functions(0)
- Logarithmic Functions(0)
- Properties of Logarithms(0)
- Exponential & Logarithmic Equations(0)
- Introduction to Trigonometric Functions(0)
- Graphs of Trigonometric Functions(0)
- Trigonometric Identities(0)
- Inverse Trigonometric Functions(0)
- 1. Limits and Continuity(0)
- 2. Intro to Derivatives(0)
- 3. Techniques of Differentiation(0)
- 4. Applications of Derivatives(0)
- 5. Graphical Applications of Derivatives(0)
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions(0)
- 7. Antiderivatives & Indefinite Integrals(0)
- 8. Definite Integrals(0)
6. Derivatives of Inverse, Exponential, & Logarithmic Functions
Derivatives of Inverse Trigonometric Functions
6. Derivatives of Inverse, Exponential, & Logarithmic Functions
Derivatives of Inverse Trigonometric Functions: Study with Video Lessons, Practice Problems & Examples
38PRACTICE PROBLEM
A lighthouse stands meters tall on a straight coastline, and a ship sails directly toward the lighthouse. Let (measured in degrees) be the angle of elevation of the lighthouse from the ship. Plot the graph of and use it to find the -coordinate where the rate of change of is maximum.
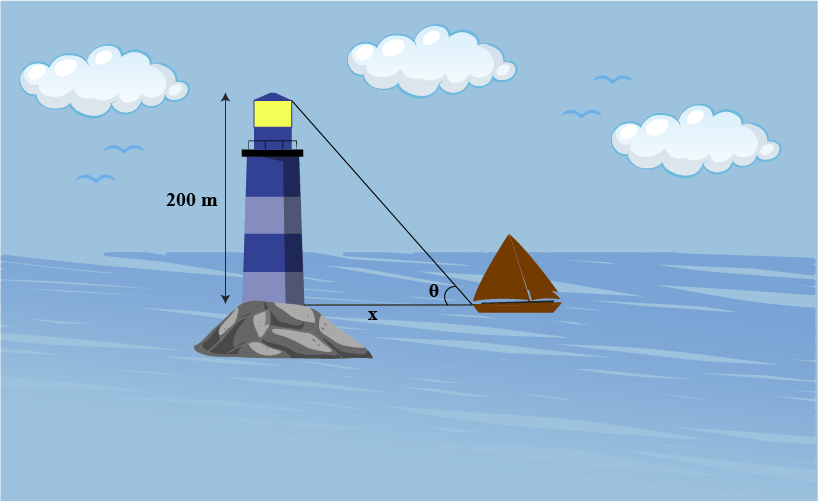
A lighthouse stands meters tall on a straight coastline, and a ship sails directly toward the lighthouse. Let (measured in degrees) be the angle of elevation of the lighthouse from the ship. Plot the graph of and use it to find the -coordinate where the rate of change of is maximum.