Table of contents
- 0. Functions(0)
- Introduction to Functions(0)
- Piecewise Functions(0)
- Properties of Functions(0)
- Common Functions(0)
- Transformations(0)
- Combining Functions(0)
- Exponent rules(0)
- Exponential Functions(0)
- Logarithmic Functions(0)
- Properties of Logarithms(0)
- Exponential & Logarithmic Equations(0)
- Introduction to Trigonometric Functions(0)
- Graphs of Trigonometric Functions(0)
- Trigonometric Identities(0)
- Inverse Trigonometric Functions(0)
- 1. Limits and Continuity(0)
- 2. Intro to Derivatives(0)
- 3. Techniques of Differentiation(0)
- 4. Applications of Derivatives(0)
- 5. Graphical Applications of Derivatives(0)
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions(0)
- 7. Antiderivatives & Indefinite Integrals(0)
- 8. Definite Integrals(0)
2. Intro to Derivatives
Tangent Lines and Derivatives
2. Intro to Derivatives
Tangent Lines and Derivatives: Study with Video Lessons, Practice Problems & Examples
70PRACTICE PROBLEM
A scientist is studying the growth of a bacterial population in a lab culture. The experiment started at AM, and the table shows the population hours since the experiment started. The population size as a function of time is modeled by the curve below.

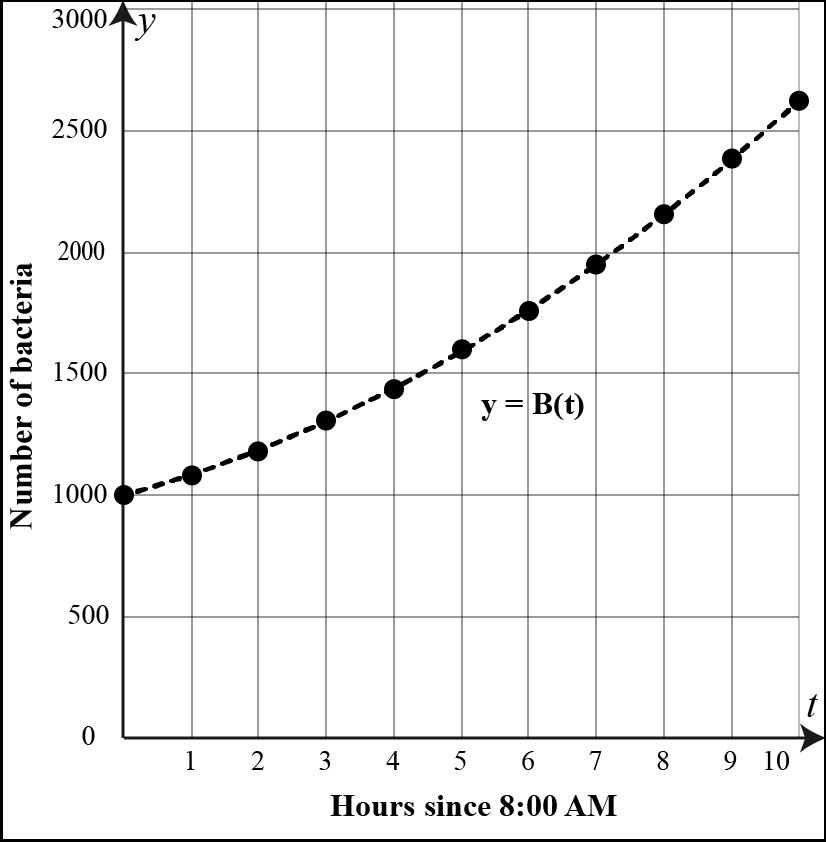
Calculate the average rate of the bacterial population growth from PM to PM.
A scientist is studying the growth of a bacterial population in a lab culture. The experiment started at AM, and the table shows the population hours since the experiment started. The population size as a function of time is modeled by the curve below.
Calculate the average rate of the bacterial population growth from PM to PM.