Table of contents
- 0. Functions(0)
- Introduction to Functions(0)
- Piecewise Functions(0)
- Properties of Functions(0)
- Common Functions(0)
- Transformations(0)
- Combining Functions(0)
- Exponent rules(0)
- Exponential Functions(0)
- Logarithmic Functions(0)
- Properties of Logarithms(0)
- Exponential & Logarithmic Equations(0)
- Introduction to Trigonometric Functions(0)
- Graphs of Trigonometric Functions(0)
- Trigonometric Identities(0)
- Inverse Trigonometric Functions(0)
- 1. Limits and Continuity(0)
- 2. Intro to Derivatives(0)
- 3. Techniques of Differentiation(0)
- 4. Applications of Derivatives(0)
- 5. Graphical Applications of Derivatives(0)
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions(0)
- 7. Antiderivatives & Indefinite Integrals(0)
- 8. Definite Integrals(0)
1. Limits and Continuity
Introduction to Limits
1. Limits and Continuity
Introduction to Limits: Study with Video Lessons, Practice Problems & Examples
3PRACTICE PROBLEM
Consider the quadratic function f(x)=−4x2+32x. Calculate the slopes of the secant lines between the points (x,f(x)) and (4,f(4)), for x=3.5,3.9,3.99,3.999. Then, make a presumption on the value of the limit of the slopes of the secant lines between (x,f(x)) and (4,f(4)) as x gets closer to 4.
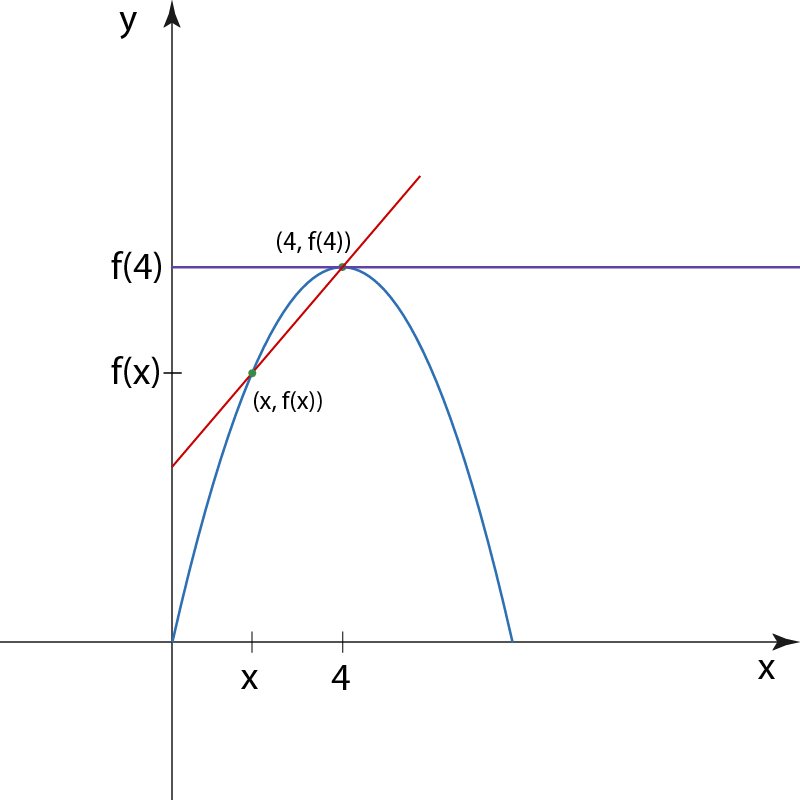
Consider the quadratic function f(x)=−4x2+32x. Calculate the slopes of the secant lines between the points (x,f(x)) and (4,f(4)), for x=3.5,3.9,3.99,3.999. Then, make a presumption on the value of the limit of the slopes of the secant lines between (x,f(x)) and (4,f(4)) as x gets closer to 4.