Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
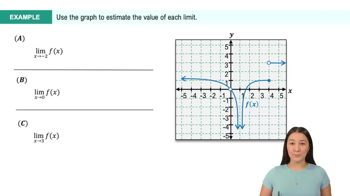
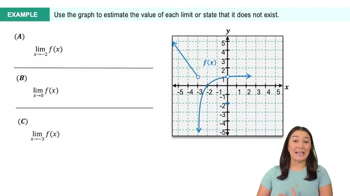
Introduction to Limits
Problem 2.4.63
Textbook Question
Use analytical methods and/or a graphing utility to identify the vertical asymptotes (if any) of the following functions.
g(θ)=tan πθ/10
 Verified step by step guidance
Verified step by step guidance1
Step 1: Recognize that the function g(θ) = tan(πθ/10) is a tangent function, which has vertical asymptotes where its argument is an odd multiple of π/2.
Step 2: Set the argument of the tangent function equal to (2n+1)π/2, where n is an integer, to find the vertical asymptotes: πθ/10 = (2n+1)π/2.
Step 3: Solve the equation from Step 2 for θ by multiplying both sides by 10/π to isolate θ: θ = (2n+1) * 5.
Step 4: Simplify the expression for θ to find the general form of the vertical asymptotes: θ = 5(2n+1).
Step 5: Conclude that the vertical asymptotes occur at θ = 5, 15, 25, ..., for n = 0, 1, 2, ..., and at θ = -5, -15, -25, ..., for n = -1, -2, -3, ..., indicating the positions of the vertical asymptotes.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning