Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
2. Intro to Derivatives
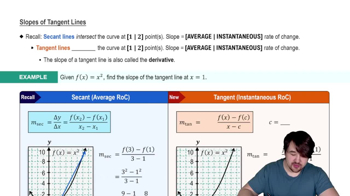
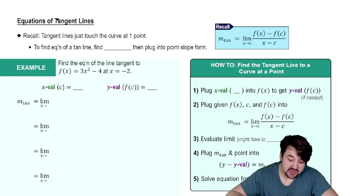
Tangent Lines and Derivatives
Problem 44
Textbook Question
Textbook QuestionAverage and marginal profit Let C(x) represent the cost of producing x items and p(x) be the sale price per item if x items are sold. The profit P(x) of selling x items is P(x) = xp(c) - C(x) (revenue minus costs). The average profit per item when x items are sold is P(x)/x and the marginal profit is dP/dx. The marginal profit approximates the profit obtained by selling one more item, given that x items have already been sold. Consider the following cost functions C and price functions p.
a. Find the profit function P.
C(x) = −0.02x²+50x+100, p(x)=100−0.1x, a=500
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Video transcript

 5:13m
5:13mWatch next
Master Slopes of Tangent Lines with a bite sized video explanation from Nick
Start learning