Graph the given function. g ( x ) = e x + 3 − 1 g\left(x\right)=e^{x+3}-1 g ( x ) = e x + 3 − 1

In this problem, we're asked to graph the given function. And here the function we have is g of x is equal to e to the power of x plus 3 minuteus 1. Now we just learned that we can treat the number e just like we would any other number, so we can also graph this exponential function just like we would any other exponential function using transformations. So let's go ahead and get started with step 0 and identify and graph our parent function. Now here in my function, I can see this e to the power of x, which represents my parent function, and I've just undergone these transformations here. So my parent function is f of x is equal to e to the power of x. And we can plot this just like we would any other exponential function. So we're going to plot this at negative one one over b, which in this case, b is e, which we know is equal to about 2.718. Now you might just want to put in your calculator 1 over e to get this value, and you'll get about 0.37. Then 1, that point still stays the same. And then 1 b, so in this case, 1 e. Now, again, we know that e is about 2.718 and so on, so I can just graph this at about 2.7 on my graph. So let's go ahead and plot these points. So negative one, getting close to that x axis there, 1, same point as always, and then one about 2.7 somewhere up here. So I can go ahead and connect this, and I know that I still have my horizontal asymptote at y equals 0, which I can plot as well using a dash line, just like any other exponential function. Now we can go ahead and start graphing our new function with transformations. Now we're first going to shift our horizontal asymptote to y equals k. Now looking at my function here, I see that it's x plus 3 minuteus 1. And now this negative one represents my vertical shift. So this is my value for k, negative 1. So I'm gonna go ahead and plot that horizontal asymptote at y equals negative one using a dash line. Now moving on to step 2, we wanna see if there's a reflection happening. Now looking at my function here, I don't have any negatives that got inserted outside or inside of my function. So I don't have to worry about a reflection here, and I can go ahead and move on to the second part of step 2, which is to shift my test points by h k. Now looking at my function, I have this x plus 3 in the exponent here, which means that my value for h is negative 3 because, remember, we consider x minus h, so this would be the same thing as x minus negative 3. So my value for h is negative 3, which represents my horizontal shift. Then we already identified k as negative one, so let's go ahead and take the points from our original function and shift them by those values. So we're gonna go ahead and shift this first point. We're gonna go 3 over to the left and then one value down. So we're gonna end up right down here. Now for my next point, I'm gonna do the same thing. Go 1, 2, 3 over and then a one down ending up right here. And then my final point to 1, 2, 3 over and then a one down, I'm gonna end up right about here. Now, I have my new points and I can go ahead and connect them using a smooth curve and approaching that asymptote. So let's go ahead and connect our new points here. Now, it's going to curve upward and then approach the asymptote towards the bottom there. So this is our new curve. Let's go ahead and identify that domain and range. Now remember, our domain is always, always going to be all real numbers. That doesn't change when we have a value of e in our exponential function. And then for our range, we need to look at whether our function is above or below our asymptote and since my asymptote is here my function is above it so that means that my range is going to go from k to infinity which in this case k is negative one so my range is from negative one to infinity. Now that we've been able to graph this exponential function let's keep going.

0. Functions

Exponential Functions

Calculus

0. Functions

Exponential Functions

Struggling with Calculus?

Join thousands of students who trust us to help them ace their exams!

Multiple Choice

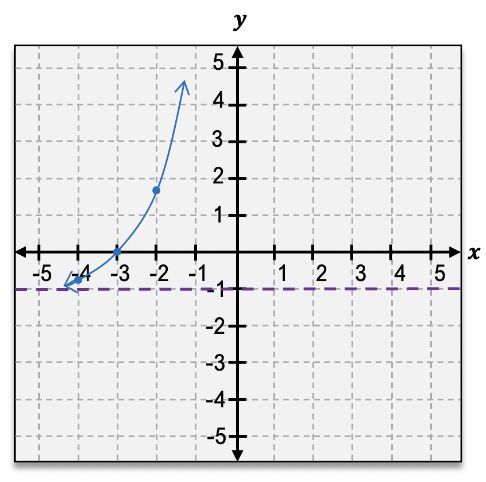
Graph the given function.
$g\left(x\right)=e^{x+3}-1$

Graph of g(x)=e^(x+3)-1 showing exponential growth.

Graph of g(x)=e^(x+3)-1 illustrating exponential growth.

Graph of g(x)=e^(x+3)-1 depicting exponential growth.

Graph of g(x)=e^(x+3)-1 showing exponential growth.

Verified step by step guidance

Identify the function to be graphed: $ g(x) = e^{x+3} - 1 $. This is an exponential function with a horizontal shift and a vertical shift.

Recognize the transformations: The function $ e^x $ is shifted horizontally to the left by 3 units due to $ x+3 $, and vertically down by 1 unit due to the $-1$.

Determine the horizontal asymptote: The horizontal asymptote of $ e^x $ is $ y = 0 $. After the vertical shift, the new horizontal asymptote is $ y = -1 $.

Plot key points: Calculate a few key points by substituting values of $ x $ into $ g(x) $. For example, when $ x = -3 $, $ g(-3) = e^{0} - 1 = 0 $. When $ x = -2 $, $ g(-2) = e^{1} - 1 $. Continue for other values to get a sense of the curve.

Sketch the graph: Draw the curve starting from the left, approaching the horizontal asymptote $ y = -1 $ as $ x $ goes to negative infinity, and rising steeply as $ x $ increases, reflecting the exponential growth.

6:13m

Watch next

Master Exponential Functions with a bite sized video explanation from Patrick

Exponential Functions practice set

Problem sets built by lead tutors

Expert video explanations

Struggling with Calculus?

Graph the given function.g(x)=ex+3−1g\left(x\right)=e^{x+3}-1g(x)=ex+3−1

Watch next

Exponential Functions practice set

Graph the given function.
$g\left(x\right)=e^{x+3}-1$