Here are the essential concepts you must grasp in order to answer the question correctly.
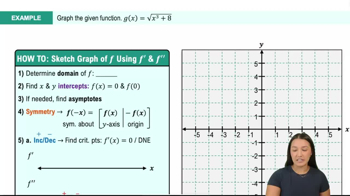
Area Under a Curve
The area under a curve represents the integral of a function over a specified interval. In this context, the area function A(x) calculates the total area between the curve y = f(t) and the t-axis from t = 0 to t = x. This concept is fundamental in calculus as it connects geometric interpretations with integral calculus.
Recommended video:
Summary of Curve Sketching Example 2
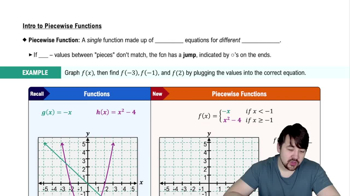
Piecewise Functions
A piecewise function is defined by different expressions based on the input value. In the given problem, f(t) is defined differently for t ≤ 3 and t > 3, which requires careful consideration when calculating the area A(6). Understanding how to evaluate piecewise functions is crucial for accurately determining the area under the curve.
Recommended video:
Definite Integrals
Definite integrals are used to compute the area under a curve between two points. To find A(6), one must evaluate the integral of f(t) from 0 to 6, taking into account the different expressions of f(t) over the relevant intervals. This concept is essential for solving problems involving area functions and understanding the accumulation of quantities.
Recommended video:
Introduction to Indefinite Integrals
 Verified step by step guidance
Verified step by step guidance Verified Solution
Verified Solution