Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Common Functions
Problem 19
Textbook Question
Textbook QuestionYeast growth Consider a colony of yeast cells that has the shape of a cylinder. As the number of yeast cells increases, the cross-sectional area A (in mm²) of the colony increases but the height of the colony remains constant. If the colony starts from a single cell, the number of yeast cells (in millions) is approximated by the linear function N(A) - CₛA, where the constant Cₛ is known as the cell-surface coefficient. Use the given information to determine the cell-surface coefficient for each of the following colonies of yeast cells, and find the number of yeast cells in the colony when the cross-sectional area A reaches 150 mm². (Source: Letters in Applied Microbiology, 594, 59, 2014)
The scientific name of baker’s or brewer’s yeast (used in making bread, wine, and beer) is Saccharomyces cerevisiae. When the cross-sectional area of a colony of this yeast reaches 100 mm², there are 571 million yeast cells.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Linear Functions
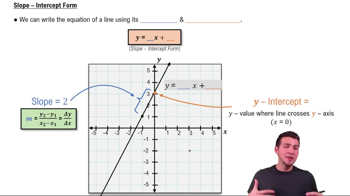
A linear function is a mathematical expression that describes a relationship between two variables, typically in the form of y = mx + b, where m is the slope and b is the y-intercept. In the context of the yeast growth question, the number of yeast cells N(A) is expressed as a linear function of the cross-sectional area A, indicating that as A increases, N(A) changes at a constant rate determined by the cell-surface coefficient Cs.
Recommended video:
Linearization
Cell-Surface Coefficient (Cs)
The cell-surface coefficient (Cs) is a constant that quantifies the relationship between the cross-sectional area of a yeast colony and the number of yeast cells it contains. It represents how many millions of cells correspond to each unit of area (mm²). Understanding Cs is crucial for calculating the number of cells in a colony based on its area, as it directly influences the linear function N(A).
Recommended video:
Example 1: Minimizing Surface Area
Cross-Sectional Area
The cross-sectional area of a cylindrical colony of yeast refers to the area of a slice taken perpendicular to the height of the cylinder. It is a critical factor in determining the growth of the yeast colony, as the problem states that while the area increases, the height remains constant. This area is essential for applying the linear function N(A) to find the number of yeast cells at specific cross-sectional measurements.
Recommended video:

Example 1: Minimizing Surface Area

 5:57m
5:57mWatch next
Master Graphs of Common Functions with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice