Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
5. Graphical Applications of Derivatives
Intro to Extrema
Problem 4.1.13
Textbook Question
Use the following graphs to identify the points (if any) on the interval [a, b] at which the function has an absolute maximum or an absolute minimum value <IMAGE>
 Verified step by step guidance
Verified step by step guidance1
Examine the graph of the function over the interval [a, b]. Identify any endpoints and critical points within this interval.
Determine the function values at the endpoints of the interval, a and b. These are potential candidates for absolute extrema.
Identify any critical points within the interval [a, b]. A critical point occurs where the derivative is zero or undefined. Check the graph for any such points.
Evaluate the function at each critical point identified in the previous step. These values are also candidates for absolute extrema.
Compare the function values obtained at the endpoints and critical points. The largest value is the absolute maximum, and the smallest value is the absolute minimum on the interval [a, b].
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
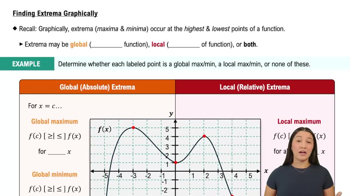
Absolute Maximum and Minimum
An absolute maximum of a function on a given interval is the highest value the function attains within that interval, while an absolute minimum is the lowest value. These extrema can occur at critical points, where the derivative is zero or undefined, or at the endpoints of the interval. Identifying these points is crucial for determining the overall behavior of the function.
Recommended video:

Finding Extrema Graphically Example 4
Critical Points
Critical points are values in the domain of a function where the derivative is either zero or does not exist. These points are significant because they are potential locations for local maxima and minima. To find absolute extrema, one must evaluate the function at these critical points as well as at the endpoints of the interval.
Recommended video:

Critical Points
Evaluating Functions on an Interval
To find absolute extrema, one must evaluate the function at all critical points and at the endpoints of the specified interval. This involves substituting these values into the function to determine which yields the highest and lowest outputs. This process ensures that all possible candidates for absolute extrema are considered.
Recommended video:

Evaluating Composed Functions

 5:58m
5:58mWatch next
Master Finding Extrema Graphically with a bite sized video explanation from Callie
Start learning