Here are the essential concepts you must grasp in order to answer the question correctly.
Definition of a Limit
The precise definition of a limit states that for a function f(x) to approach a limit L as x approaches a value c, for every ε > 0, there must exist a δ > 0 such that if 0 < |x - c| < δ, then |f(x) - L| < ε. This formal definition is crucial for proving limits rigorously.
Recommended video:
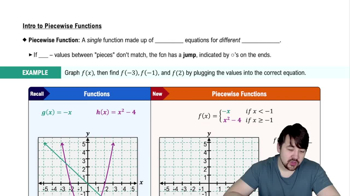
Piecewise Functions
A piecewise function is defined by different expressions based on the input value. In this case, f(x) has two definitions: 3x - 12 for x ≤ 7 and x + 2 for x > 7. Understanding how to evaluate limits at points where the function changes its definition is essential for solving the limit problem.
Recommended video:
Epsilon-Delta Proof
An epsilon-delta proof involves demonstrating that for any chosen ε, a corresponding δ can be found that satisfies the limit definition. This method is used to show that as x approaches a certain value, the function's output can be made arbitrarily close to the limit, thus confirming the limit's existence.
Recommended video:
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 6:47m
6:47m