Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
Introduction to Limits
Problem 51b
Textbook Question
Textbook QuestionAnalyze the following limits. Then sketch a graph of y=tanx with the window [−π,π]×[−10,10]and use your graph to check your work.
lim x→π/2^− tan x
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
A limit is a fundamental concept in calculus that describes the behavior of a function as its input approaches a certain value. It helps in understanding the function's behavior near points of interest, including points where the function may not be defined. For example, the limit of tan(x) as x approaches π/2 from the left indicates how the function behaves as it nears this vertical asymptote.
Recommended video:

One-Sided Limits
Vertical Asymptotes
Vertical asymptotes occur in functions where the function approaches infinity or negative infinity as the input approaches a certain value. For the tangent function, vertical asymptotes are found at odd multiples of π/2, where the function is undefined. Understanding vertical asymptotes is crucial for analyzing the limits of functions like tan(x) and for sketching accurate graphs.
Recommended video:
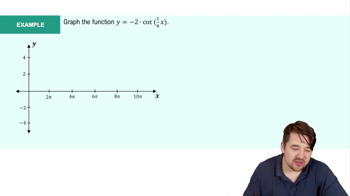
Introduction to Cotangent Graph Example 1
Graphing Trigonometric Functions
Graphing trigonometric functions, such as y = tan(x), involves understanding their periodic nature and key features like asymptotes, intercepts, and periodicity. The tangent function has a period of π and exhibits vertical asymptotes at odd multiples of π/2. By sketching the graph within a specified window, one can visually confirm the behavior of the function and the accuracy of calculated limits.
Recommended video:

Introduction to Trigonometric Functions

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning