Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Inverse Trigonometric Functions
Problem 4.2.34
Textbook Question
An inverse tangent identity
b. Prove that tan⁻¹ x + tan⁻¹ x(1/x) = π/2, for x > 0.
 Verified step by step guidance
Verified step by step guidance1
Start by recalling the inverse tangent identity: \( \tan^{-1}(x) + \tan^{-1}(y) = \tan^{-1}\left(\frac{x + y}{1 - xy}\right) \) when \( xy < 1 \).
In this problem, set \( y = \frac{1}{x} \). Substitute \( y \) into the identity: \( \tan^{-1}(x) + \tan^{-1}\left(\frac{1}{x}\right) = \tan^{-1}\left(\frac{x + \frac{1}{x}}{1 - x \cdot \frac{1}{x}}\right) \).
Simplify the expression inside the inverse tangent: \( \frac{x + \frac{1}{x}}{1 - 1} = \frac{x + \frac{1}{x}}{0} \).
Recognize that the denominator becomes zero, which implies the expression approaches infinity. The inverse tangent of infinity is \( \frac{\pi}{2} \).
Conclude that \( \tan^{-1}(x) + \tan^{-1}\left(\frac{1}{x}\right) = \frac{\pi}{2} \) for \( x > 0 \), as the expression inside the inverse tangent approaches infinity.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
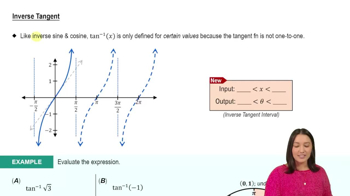
Inverse Tangent Function
The inverse tangent function, denoted as tan⁻¹(x) or arctan(x), is the function that returns the angle whose tangent is x. It is defined for all real numbers and has a range of (-π/2, π/2). Understanding this function is crucial for manipulating and proving identities involving angles.
Recommended video:
Inverse Tangent
Trigonometric Identities
Trigonometric identities are equations that involve trigonometric functions and are true for all values of the variables involved. One important identity is that the sum of the angles whose tangents are x and 1/x equals π/2, which reflects the complementary nature of these angles. This identity is essential for proving the given statement.
Recommended video:

Verifying Trig Equations as Identities
Complementary Angles
Complementary angles are two angles whose sum is π/2 radians (or 90 degrees). In the context of the problem, if θ = tan⁻¹(x), then the angle whose tangent is 1/x is π/2 - θ. Recognizing this relationship is key to proving the identity tan⁻¹(x) + tan⁻¹(1/x) = π/2 for x > 0.
Recommended video:
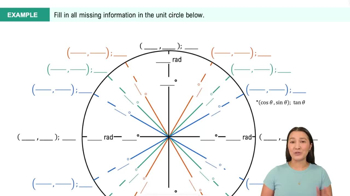
Trig Values in Quadrants II, III, & IV Example 2
Related Videos
Related Practice