Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
A limit is a fundamental concept in calculus that describes the behavior of a function as its input approaches a certain value. It helps in understanding how functions behave near points of interest, including points where they may not be defined. For example, the limit of √x as x approaches 0 examines the value that √x approaches as x gets closer to 0.
Recommended video:
Square Root Function
The square root function, denoted as √x, is defined for non-negative values of x and returns the non-negative value whose square is x. This function is continuous and increases as x increases. Understanding its graph is crucial for analyzing limits, especially as it approaches 0, where the function's behavior can be visually interpreted.
Recommended video:
Multiplying & Dividing Functions
Graphical Interpretation
Graphical interpretation involves analyzing the visual representation of a function to understand its behavior. For the function y = √x, the graph is a curve that starts at the origin (0,0) and rises to the right. By examining this graph, one can intuitively grasp how the function behaves as x approaches 0, which aids in determining the limit.
Recommended video:
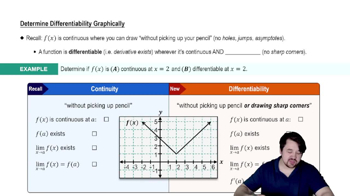
Determining Differentiability Graphically
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 6:47m
6:47m