Based on the graph of f ( x ) f\left(x\right) f ( x ) , describe the graph of the derivative f ′ ( x ) f^{\prime}\left(x\right) f ′ ( x ) on the interval ( 0 , ∞ ) \left(0,\infty\right) ( 0 , ∞ ) .

So in this problem, we're told based on the graph f of x, describe the graph of the derivative f prime of x on the interval from 0 to infinity. So, basically, what we're doing is looking at this portion of the graph from 0 to infinity, and this would just keep going on. We're asked what the derivative is going to look like. Now I'm going to sketch kind of a basic graph of our derivative over here, and it's not gonna be like something with a lot of detail per se. I'm just going to focus on what this is gonna look like. So we'd have some kind of graph like this. And this is our graph where we have x and y, and we're trying to graph a function f prime of x. Now to draw f prime of x, we're only gonna focus on this side of the graph since that's where the interval is from 0 to infinity. And what I need to do is take a look at how this curve behaves and draw some tangent lines to see what it's gonna look like. Now if I go ahead and draw a tangent line right about here, notice that we get a tangent line with a positive slope. Because we got a positive slope, that means we're going to be above the x axis. And then if I go ahead and draw another tangent line here, we get another positive slope except this one is more steep. So you're going to be farther above the x axis. And you can actually keep drawing tangent lines at different points on this graph, and it'll only have positive slopes that keep getting more and more steep. So because of that, it becomes pretty clear what the graph is going to look like. And based on what this graph looks like on the interval from 0 to infinity, we can see that everything is going to be above the x axis. So we can describe this graph as being a line that looks something like this, but if we're just talking about where this graph is with reference to the x axis, we would say that this is above the x axis. So this is how we can describe what this graph looks like or what the derivative looks like based on the function we have, and that would be the solution to this problem. So hope you found this video helpful, and let's move on.

2. Intro to Derivatives

Basic Graphing of the Derivative

Calculus

2. Intro to Derivatives

Basic Graphing of the Derivative

Struggling with Calculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

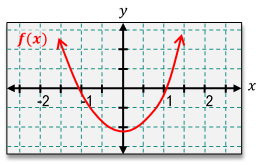
Based on the graph of $f\left(x\right)$ , describe the graph of the derivative $f^{\prime}\left(x\right)$ on the interval $\left(0,\infty\right)$ .

Below the x-axis

Above the x-axis

On the x-axis

Verified step by step guidance

Observe the graph of f(x). It appears to be a parabola opening upwards, which suggests that f(x) is a quadratic function.

Identify the behavior of f(x) on the interval (0,∞). The graph is increasing throughout this interval.

Recall that the derivative f′(x) represents the slope of the tangent line to the graph of f(x) at any point x. Since f(x) is increasing on (0,∞), f′(x) will be positive on this interval.

Consider the shape of the graph. Since it is a parabola, the derivative f′(x) will be a linear function. For a parabola opening upwards, the derivative is a positive linear function.

Conclude that on the interval (0,∞), the graph of the derivative f′(x) will be above the x-axis, indicating positive values.

6:15m

Watch next

Master Graphing The Derivative with a bite sized video explanation from Nick

Start learning

Struggling with Calculus?

Based on the graph of ﻿f(x)f\left(x\right)f(x)﻿, describe the graph of the derivative ﻿f′(x)f^{\prime}\left(x\right)f′(x)﻿ on the interval ﻿(0,∞)\left(0,\infty\right)(0,∞)﻿.

Watch next

Based on the graph of $f\left(x\right)$ , describe the graph of the derivative $f^{\prime}\left(x\right)$ on the interval $\left(0,\infty\right)$ .