Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
Introduction to Limits
Problem 2.32a
Textbook Question
Textbook QuestionA rock is dropped off the edge of a cliff, and its distance s (in feet) from the top of the cliff after t seconds is s(t)=16t^2. Assume the distance from the top of the cliff to the ground is 96 ft.
a. When will the rock strike the ground?
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Quadratic Functions
The function s(t) = 16t^2 is a quadratic function, which represents a parabolic relationship between time t and distance s. In this context, it models the distance fallen by the rock over time due to gravity. Understanding the properties of quadratic functions, such as their vertex and roots, is essential for determining when the rock will hit the ground.
Recommended video:

Introduction to Polynomial Functions
Roots of Equations
Finding when the rock strikes the ground involves solving for the roots of the equation s(t) = 16t^2. The roots represent the values of t when the distance s equals zero, indicating the moment the rock reaches the ground. This requires setting the equation equal to the height of the cliff (96 ft) and solving for t.
Recommended video:
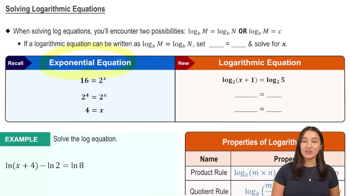
Solving Logarithmic Equations
Physical Interpretation of Motion
In this scenario, the physical interpretation of motion under gravity is crucial. The equation s(t) = 16t^2 derives from the physics of free fall, where the distance fallen is proportional to the square of the time elapsed. Recognizing this relationship helps in understanding the implications of the calculated time when the rock strikes the ground.
Recommended video:

Derivatives Applied To Velocity

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning