Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Introduction to Functions
Problem 4.R.118a
Textbook Question
{Use of Tech} A family of superexponential functions Let ƒ(x) = (a + x)ˣ , where a > 0.
a. What is the domain of f (in terms of a)?
 Verified step by step guidance
Verified step by step guidance1
To determine the domain of the function \( f(x) = (a + x)^x \), we need to identify the values of \( x \) for which the expression is defined.
The expression \( (a + x)^x \) is defined when \( a + x > 0 \) because the base of the power must be positive for real number exponents.
Solve the inequality \( a + x > 0 \) to find the values of \( x \). This gives \( x > -a \).
Therefore, the domain of \( f(x) \) in terms of \( a \) is all real numbers \( x \) such that \( x > -a \).
In interval notation, the domain is \( (-a, \infty) \).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain of a Function
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. For the function f(x) = (a + x)ˣ, where a > 0, the domain is determined by the values of x that keep the expression a + x positive, as the base of an exponent must be positive for real-valued outputs.
Recommended video:
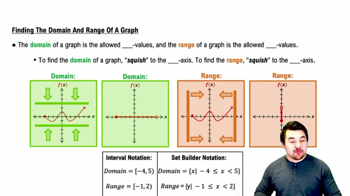
Finding the Domain and Range of a Graph
Exponential Functions
Exponential functions are mathematical expressions in the form f(x) = bˣ, where b is a positive constant. In the case of f(x) = (a + x)ˣ, the function exhibits superexponential growth, meaning it grows faster than any polynomial function as x increases. Understanding the behavior of exponential functions is crucial for analyzing their domains and ranges.
Recommended video:

Exponential Functions
Inequalities
Inequalities are mathematical statements that compare two expressions, indicating whether one is greater than, less than, or equal to the other. In determining the domain of f(x) = (a + x)ˣ, we need to solve the inequality a + x > 0, which leads to x > -a. This understanding of inequalities is essential for identifying valid input values for the function.
Recommended video:

Finding the Domain and Range of a Graph

 1:36m
1:36mWatch next
Master Introduction to Calculus Channel with a bite sized video explanation from Callie
Start learning