Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Common Functions
Problem 15.
Textbook Question
Textbook QuestionEvaluate cos⁻¹(cos(5π/4)).
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Inverse Trigonometric Functions
Inverse trigonometric functions, such as cos⁻¹(x), are used to find the angle whose cosine is x. These functions have specific ranges; for cos⁻¹(x), the output is restricted to the interval [0, π]. This means that when evaluating cos⁻¹(cos(θ)), the result will depend on the angle θ and its position within the defined range.
Recommended video:

Derivatives of Other Inverse Trigonometric Functions
Cosine Function and Its Periodicity
The cosine function is periodic with a period of 2π, meaning that cos(θ) = cos(θ + 2kπ) for any integer k. This periodicity implies that angles can be expressed in multiple equivalent forms. For example, cos(5π/4) can be simplified by recognizing that it is equivalent to cos(5π/4 - 2π) = cos(-3π/4), which helps in evaluating the inverse function.
Recommended video:

Graph of Sine and Cosine Function
Quadrants and Reference Angles
Understanding the unit circle and the quadrants is essential for evaluating trigonometric functions. The angle 5π/4 is located in the third quadrant, where cosine values are negative. The reference angle for 5π/4 is π/4, which helps in determining the cosine value, as cos(5π/4) = -√2/2. This knowledge is crucial for correctly applying the inverse function.
Recommended video:
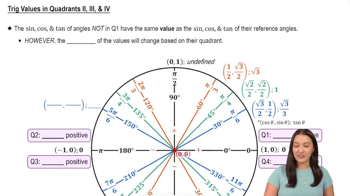
Trig Values in Quadrants II, III, & IV

 5:57m
5:57mWatch next
Master Graphs of Common Functions with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice