Here are the essential concepts you must grasp in order to answer the question correctly.
Inverse Trigonometric Functions
Inverse trigonometric functions, such as cos⁻¹(x), are used to find the angle whose cosine is x. These functions have specific ranges; for cos⁻¹(x), the output is restricted to the interval [0, π]. This means that when evaluating cos⁻¹(cos(θ)), the result will depend on the angle θ and its position within the defined range.
Recommended video:
Derivatives of Other Inverse Trigonometric Functions
Cosine Function and Its Periodicity
The cosine function is periodic with a period of 2π, meaning that cos(θ) = cos(θ + 2kπ) for any integer k. This periodicity implies that angles can be expressed in multiple equivalent forms. For example, cos(5π/4) can be simplified by recognizing that it is equivalent to cos(5π/4 - 2π) = cos(-3π/4), which helps in evaluating the inverse function.
Recommended video:
Graph of Sine and Cosine Function
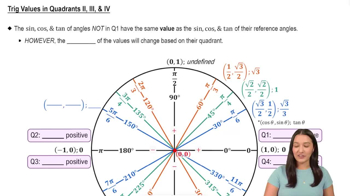
Quadrants and Reference Angles
Understanding the unit circle and the quadrants is essential for evaluating trigonometric functions. The angle 5π/4 is located in the third quadrant, where cosine values are negative. The reference angle for 5π/4 is π/4, which helps in determining the cosine value, as cos(5π/4) = -√2/2. This knowledge is crucial for correctly applying the inverse function.
Recommended video:
Trig Values in Quadrants II, III, & IV