Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Common Functions
Problem 65c
Textbook Question
Textbook Question{Use of Tech} Height and time The height in feet of a baseball hit straight up from the ground with an initial velocity of 64 ft/s is given by h= ƒ(t) = 64t - 16t² where t is measured in seconds after the hit.
c. Find the inverse function that gives the time t at which the ball is at height h as the ball travels downward. Express your answer in the form t = ƒ⁻¹ (h)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
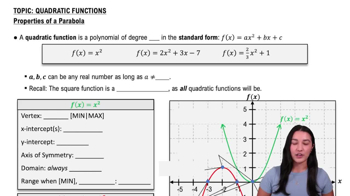
Quadratic Functions
The height function h(t) = 64t - 16t² is a quadratic function, which is characterized by its parabolic shape. Quadratic functions can be expressed in the standard form ax² + bx + c, where a, b, and c are constants. Understanding the properties of quadratic functions, such as their vertex, axis of symmetry, and roots, is essential for analyzing their behavior, including finding inverse functions.
Recommended video:

Introduction to Polynomial Functions
Inverse Functions
An inverse function essentially reverses the effect of the original function. For a function f(t), its inverse f⁻¹(h) allows us to find the input t for a given output h. To find the inverse of a function, one typically swaps the dependent and independent variables and solves for the new dependent variable. This concept is crucial for determining the time t at which the baseball reaches a specific height h.
Recommended video:

Inverse Cosine
Solving Quadratic Equations
To find the inverse function in this context, one must solve the quadratic equation derived from the height function. This often involves rearranging the equation to isolate t, which may require using the quadratic formula, t = (-b ± √(b² - 4ac)) / 2a. Understanding how to manipulate and solve quadratic equations is vital for accurately determining the time at which the baseball reaches a given height as it travels downward.
Recommended video:
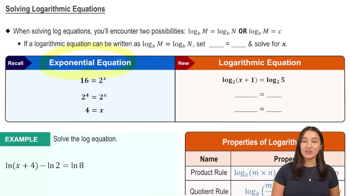
Solving Logarithmic Equations

 5:57m
5:57mWatch next
Master Graphs of Common Functions with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice