Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
2. Intro to Derivatives
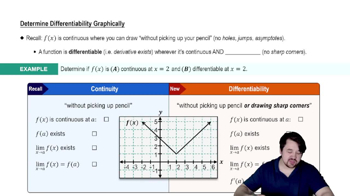
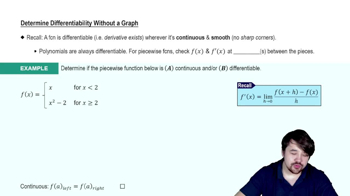
Differentiability
Problem 3.2.8
Textbook Question
If f is continuous at a, must f be differentiable at a?
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the definitions: A function f is continuous at a point a if the limit of f(x) as x approaches a is equal to f(a). A function is differentiable at a if the derivative f'(a) exists, which means the limit of [f(x) - f(a)] / (x - a) as x approaches a exists.
Step 2: Consider the relationship: Differentiability implies continuity. If a function is differentiable at a point, it must be continuous at that point. However, the reverse is not necessarily true; continuity does not imply differentiability.
Step 3: Explore a counterexample: A classic example is the absolute value function f(x) = |x|. This function is continuous everywhere, including at x = 0, but it is not differentiable at x = 0 because the slope of the tangent line is not defined (the left-hand and right-hand derivatives are not equal).
Step 4: Analyze the counterexample: For f(x) = |x|, as x approaches 0 from the left, the slope of the tangent line approaches -1, and from the right, it approaches 1. Since these two one-sided limits are not equal, the derivative at x = 0 does not exist.
Step 5: Conclude: Therefore, a function can be continuous at a point but not differentiable at that point. Continuity at a point does not guarantee differentiability at that point.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mPlay a video:
Was this helpful?

 5:02m
5:02mWatch next
Master Determining Differentiability Graphically with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice