Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
1. Limits and Continuity
Introduction to Limits
Problem 2.7.49
Textbook Question
Determine whether the following statements are true and give an explanation or counterexample. Assume a and L are finite numbers and assume lim x→a f(x) =L
d. If |x−a|<δ, then a−δ<x<a+δ.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the statement: The statement is about the definition of the limit of a function as x approaches a. It involves the concept of a delta (δ) neighborhood around the point a.
Step 2: Recall the definition of a limit: The limit of f(x) as x approaches a is L, written as \( \lim_{{x \to a}} f(x) = L \), if for every \( \epsilon > 0 \), there exists a \( \delta > 0 \) such that if \( 0 < |x - a| < \delta \), then \( |f(x) - L| < \epsilon \).
Step 3: Analyze the given condition: The condition \( |x - a| < \delta \) implies that x is within a distance δ from a. This means x is in the interval (a - δ, a + δ).
Step 4: Verify the statement: The statement 'If \( |x - a| < \delta \), then \( a - \delta < x < a + \delta \)' is indeed true by the definition of absolute value and the concept of a δ-neighborhood.
Step 5: Conclusion: The statement is true because it directly follows from the definition of the absolute value and the concept of a δ-neighborhood around a point a.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Limit of a Function
The limit of a function describes the behavior of the function as the input approaches a certain value. In this case, lim x→a f(x) = L means that as x gets closer to a, the function f(x) approaches the value L. Understanding limits is crucial for analyzing continuity and the behavior of functions near specific points.
Recommended video:

Limits of Rational Functions: Denominator = 0
Delta-Epsilon Definition of a Limit
The delta-epsilon definition formalizes the concept of limits. It states that for every ε (epsilon) greater than 0, there exists a δ (delta) such that if |x - a| < δ, then |f(x) - L| < ε. This definition is essential for proving the validity of limits and understanding the precise conditions under which a function approaches a limit.
Recommended video:

Definition of the Definite Integral
Inequalities and Intervals
Inequalities are used to describe the range of values that a variable can take. The statement |x - a| < δ implies that x lies within the interval (a - δ, a + δ). Understanding how to manipulate and interpret these inequalities is vital for analyzing the behavior of functions in the context of limits and continuity.
Recommended video:
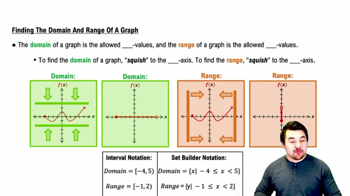
Finding the Domain and Range of a Graph

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning