Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Exponential & Logarithmic Equations
Problem 1.85
Textbook Question
Finding all inverses Find all the inverses associated with the following functions, and state their domains.
ƒ(x) = x² -2x + 6
 Verified step by step guidance
Verified step by step guidance1
<Step 1: Determine if the function is one-to-one.> To find the inverse of a function, it must be one-to-one. The function \( f(x) = x^2 - 2x + 6 \) is a quadratic function, which is not one-to-one over all real numbers. Therefore, we need to restrict the domain to make it one-to-one. Quadratic functions are one-to-one on intervals where they are either strictly increasing or strictly decreasing. Since the parabola opens upwards, we can consider the vertex to find the interval. The vertex form of a quadratic function is \( f(x) = a(x-h)^2 + k \), where \( (h, k) \) is the vertex.>
<Step 2: Find the vertex of the quadratic function.> The vertex of \( f(x) = x^2 - 2x + 6 \) can be found using the formula \( h = -\frac{b}{2a} \). Here, \( a = 1 \) and \( b = -2 \), so \( h = -\frac{-2}{2 \times 1} = 1 \). Substitute \( x = 1 \) into the function to find \( k \): \( f(1) = 1^2 - 2 \times 1 + 6 = 5 \). Thus, the vertex is \( (1, 5) \).>
<Step 3: Restrict the domain.> To make the function one-to-one, restrict the domain to either \( x \leq 1 \) or \( x \geq 1 \). This will ensure the function is either strictly increasing or strictly decreasing. For this problem, let's choose \( x \geq 1 \) for simplicity, where the function is increasing.>
<Step 4: Solve for the inverse function.> To find the inverse, swap \( x \) and \( y \) in the equation \( y = x^2 - 2x + 6 \) and solve for \( y \). This gives \( x = y^2 - 2y + 6 \). Rearrange to form a quadratic equation in terms of \( y \): \( y^2 - 2y + (6 - x) = 0 \). Use the quadratic formula \( y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) to solve for \( y \). Here, \( a = 1 \), \( b = -2 \), and \( c = 6 - x \).>
<Step 5: State the inverse function and its domain.> The inverse function will be \( f^{-1}(x) = 1 + \sqrt{x - 5} \) for \( x \geq 5 \), since we chose the domain \( x \geq 1 \) for the original function. The domain of the inverse function is determined by the range of the original function, which is \( y \geq 5 \).>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Inverse Functions
An inverse function essentially reverses the effect of the original function. If a function f takes an input x and produces an output y, the inverse function f⁻¹ takes y back to x. To find an inverse, one typically swaps the roles of x and y in the equation and solves for y.
Recommended video:

Inverse Cosine
Domain and Range
The domain of a function is the set of all possible input values (x-values) that the function can accept, while the range is the set of all possible output values (y-values). When finding the inverse of a function, the domain of the original function becomes the range of the inverse, and vice versa.
Recommended video:
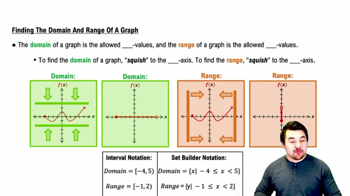
Finding the Domain and Range of a Graph
Completing the Square
Completing the square is a method used to transform a quadratic function into a perfect square trinomial, which makes it easier to analyze and find its vertex. This technique is particularly useful for rewriting the function in vertex form, aiding in the identification of its inverse and determining its domain.
Recommended video:
Trig Values in Quadrants II, III, & IV Example 1

 4:46m
4:46mWatch next
Master Solving Exponential Equations Using Like Bases with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice