Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
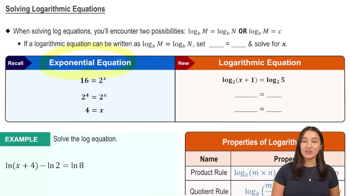
Exponential & Logarithmic Equations
Problem 1.57
Textbook Question
Textbook QuestionSolving equations Solve the following equations.
7ˣ = 21
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Exponential Functions
Exponential functions are mathematical expressions in the form of f(x) = a * b^x, where 'a' is a constant, 'b' is the base, and 'x' is the exponent. In the equation 7ˣ = 21, we are dealing with an exponential function where the variable 'x' is in the exponent. Understanding the properties of exponential functions is crucial for solving equations involving them.
Recommended video:

Exponential Functions
Logarithms
Logarithms are the inverse operations of exponentiation, allowing us to solve for the exponent in equations like 7ˣ = 21. The logarithm log_b(a) answers the question: to what exponent must the base 'b' be raised to produce 'a'? In this case, we can use logarithms to isolate 'x' by rewriting the equation in logarithmic form.
Recommended video:

Logarithms Introduction
Properties of Equality
The properties of equality state that if two expressions are equal, then we can perform the same operation on both sides without changing the equality. This principle is essential when manipulating equations, such as applying logarithms to both sides of 7ˣ = 21 to solve for 'x'. Understanding these properties ensures that the solutions derived from the equations are valid.
Recommended video:

Properties of Functions

 4:46m
4:46mWatch next
Master Solving Exponential Equations Using Like Bases with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice