Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Introduction to Functions
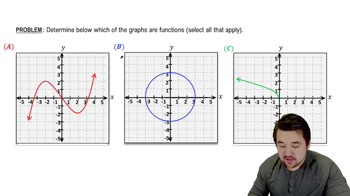
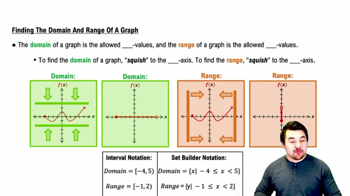
Problem 1.17
Textbook Question
Textbook QuestionThe National Weather Service releases approximately 70,000 radiosondes every year to collect data from the atmosphere. Attached to a balloon, a radiosonde rises at about 1000 ft/min until the balloon bursts in the upper atmosphere. Suppose a radiosonde is released from a point 6 ft above the ground and that 5 seconds later, it is 83 ft above the ground. Let f(t) represent the height (in feet) that the radiosonde is above the ground t seconds after it is released. Evaluate 5−0f(5)−f(0) and interpret the meaning of this quotient.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
19
views
Was this helpful?