Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
4. Applications of Derivatives
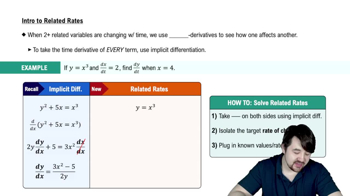
Related Rates
Problem 3.7.105b
Textbook Question
{Use of Tech} Power and energy The total energy in megawatt-hr (MWh) used by a town is given by E(t) = 400t+2400/π sin πt/12, where t≥0 is measured in hours, with t=0 corresponding to noon.
b. At what time of day is the rate of energy consumption a maximum? What is the power at that time of day?
 Verified step by step guidance
Verified step by step guidance1
Step 1: To find the time of day when the rate of energy consumption is a maximum, we need to find the derivative of the energy function E(t) with respect to time t. This derivative, E'(t), represents the rate of energy consumption, also known as power.
Step 2: Differentiate E(t) = 400t + \frac{2400}{\pi} \sin\left(\frac{\pi t}{12}\right) with respect to t. Use the derivative rules: the derivative of 400t is 400, and for the sine term, use the chain rule. The derivative of \sin\left(\frac{\pi t}{12}\right) is \cos\left(\frac{\pi t}{12}\right) \cdot \frac{\pi}{12}.
Step 3: Set the derivative E'(t) equal to zero to find the critical points. This will help us determine when the rate of energy consumption is at a maximum or minimum. Solve the equation 400 + \frac{2400}{\pi} \cdot \cos\left(\frac{\pi t}{12}\right) \cdot \frac{\pi}{12} = 0 for t.
Step 4: Solve the equation from Step 3 for t to find the critical points. This involves isolating the cosine term and using inverse trigonometric functions to find the values of t that satisfy the equation.
Step 5: Evaluate the second derivative, E''(t), to determine the concavity at the critical points found in Step 4. If E''(t) is negative at a critical point, it indicates a local maximum. Use this information to identify the time of day when the rate of energy consumption is a maximum.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
8mPlay a video:
Was this helpful?
Related Videos
Related Practice