Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
Finding Limits Algebraically
Problem 99
Textbook Question
Textbook QuestionEvaluate lim x→1 3√x − 1 / x (Hint: x−1=(3√x)^3−1^3.)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Limits
In calculus, a limit is a fundamental concept that describes the behavior of a function as its input approaches a certain value. It helps in understanding the function's value at points where it may not be explicitly defined. Evaluating limits is crucial for determining continuity, derivatives, and integrals.
Recommended video:

One-Sided Limits
Factoring and Rationalization
Factoring involves rewriting an expression as a product of its factors, which can simplify the evaluation of limits. In this case, the hint suggests using the difference of cubes formula to factor the expression. Rationalization is a technique used to eliminate roots from the denominator, making it easier to compute limits.
Recommended video:
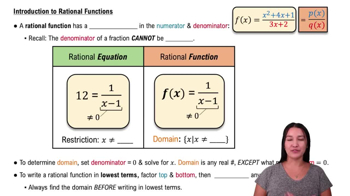
Intro to Rational Functions
The Difference of Cubes Formula
The difference of cubes formula states that a³ - b³ = (a - b)(a² + ab + b²). This formula is useful for simplifying expressions where one term is a cube, as it allows us to factor the expression and potentially cancel terms, facilitating the evaluation of limits.
Recommended video:

The Power Rule: Negative & Rational Exponents Example 2

 5:21m
5:21mWatch next
Master Finding Limits by Direct Substitution with a bite sized video explanation from Callie
Start learningRelated Videos
Related Practice







