Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Introduction to Functions
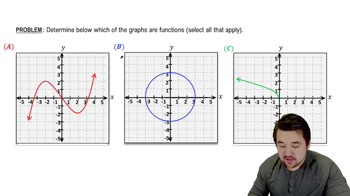
Problem 75b
Textbook Question
A GPS device tracks the elevation E (in feet) of a hiker walking in the mountains. The elevation t hours after beginning the hike is given in the figure. <IMAGE>
Repeat the procedure outlined in part (a) for the secant line that passes through points P and Q.
 Verified step by step guidance
Verified step by step guidance1
Identify the coordinates of points P and Q on the graph. These points represent the elevation at specific times during the hike.
Determine the coordinates of point P, which is given as (t1, E1), where t1 is the time in hours and E1 is the elevation in feet at that time.
Determine the coordinates of point Q, which is given as (t2, E2), where t2 is the time in hours and E2 is the elevation in feet at that time.
Use the formula for the slope of a secant line, which is (E2 - E1) / (t2 - t1), to calculate the average rate of change of elevation between points P and Q.
Interpret the slope of the secant line as the average rate of change of elevation with respect to time between the two points, providing insight into the hiker's change in elevation over that interval.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?

 1:36m
1:36mWatch next
Master Introduction to Calculus Channel with a bite sized video explanation from Callie
Start learning