Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
2. Intro to Derivatives
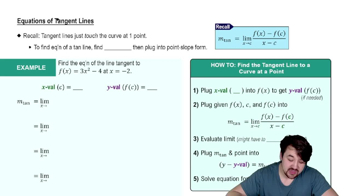
Tangent Lines and Derivatives
Problem 3.2.73a
Textbook Question
Vertical tangent lines If a function f is continuous at a and lim x→a| f′(x)|=∞, then the curve y=f(x) has a vertical tangent line at a, and the equation of the tangent line is x=a. If a is an endpoint of a domain, then the appropriate one-sided derivative (Exercises 71–72) is used. Use this information to answer the following questions.
73. {Use of Tech} Graph the following functions and determine the location of the vertical tangent lines.
a. f(x) = (x-2)^1/3
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the problem statement. We need to determine where the function f(x) = (x-2)^{1/3} has vertical tangent lines by analyzing the behavior of its derivative.
Step 2: Find the derivative of the function f(x) = (x-2)^{1/3}. Use the power rule for derivatives, which states that if f(x) = x^n, then f'(x) = n*x^{n-1}.
Step 3: Apply the power rule to f(x) = (x-2)^{1/3}. The derivative f'(x) will be (1/3)*(x-2)^{-2/3}.
Step 4: Analyze the behavior of f'(x) as x approaches the point of interest, which is x = 2. Specifically, evaluate the limit lim_{x→2} |f'(x)| to determine if it approaches infinity.
Step 5: Conclude that if lim_{x→2} |f'(x)| = ∞, then there is a vertical tangent line at x = 2. The equation of this vertical tangent line is x = 2.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Vertical Tangent Lines
A vertical tangent line occurs at a point on a curve where the slope of the tangent approaches infinity. This typically indicates that the function is changing very rapidly at that point, leading to a vertical orientation of the tangent line. Mathematically, this is represented by the condition that the limit of the derivative approaches infinity as x approaches the point of tangency.
Recommended video:
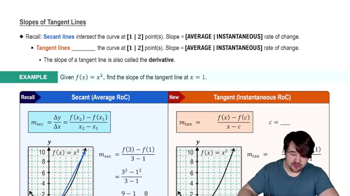
Slopes of Tangent Lines
Continuity and Derivatives
For a function to have a vertical tangent line at a point, it must be continuous at that point. Additionally, the behavior of the derivative is crucial; if the limit of the absolute value of the derivative approaches infinity as x approaches the point, it confirms the presence of a vertical tangent. This relationship between continuity and the behavior of derivatives is fundamental in calculus.
Recommended video:

Intro to Continuity
One-Sided Derivatives
One-sided derivatives are used to analyze the behavior of a function at endpoints of its domain or at points where the function may not be differentiable in the traditional sense. The left-hand derivative and right-hand derivative provide insights into the slope of the function from either side of a point, which is essential for determining the nature of the tangent line at that point, especially in cases of vertical tangents.
Recommended video:

One-Sided Limits

 5:13m
5:13mWatch next
Master Slopes of Tangent Lines with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice