Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals3h 25m
4. Applications of Derivatives
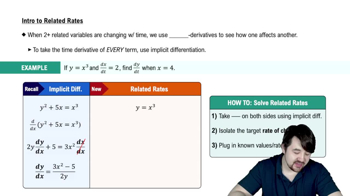
Related Rates
Problem 3.11.60
Textbook Question
A ship leaves port traveling southwest at a rate of 12 mi/hr. At noon, the ship reaches its closest approach to a radar station, which is on the shore 1.5 mi from the port. If the ship maintains its speed and course, what is the rate of change of the tracking angle θ between the radar station and the ship at 1:30 P.M. (see figure)? (Hint: Use the Law of Sines.) <IMAGE>
 Verified step by step guidance
Verified step by step guidance1
Identify the position of the ship at noon and at 1:30 P.M. The ship travels southwest at 12 mi/hr, so after 1.5 hours, it will have traveled 12 mi/hr * 1.5 hr = 18 miles southwest from its closest point to the radar station.
Draw a right triangle where one vertex is the radar station, another is the port, and the third is the position of the ship at 1:30 P.M. The distance from the radar station to the port is 1.5 miles, and the distance from the radar station to the ship can be calculated using the Pythagorean theorem.
Use the Law of Sines to relate the sides of the triangle to the angles. The Law of Sines states that (a/sin(A)) = (b/sin(B)) = (c/sin(C)), where a, b, and c are the lengths of the sides opposite to angles A, B, and C respectively.
Differentiate the relationship obtained from the Law of Sines with respect to time to find the rate of change of the angle θ. This will involve implicit differentiation and applying the chain rule.
Substitute the known values into the differentiated equation to find the rate of change of the angle θ at 1:30 P.M.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
11mPlay a video:
Was this helpful?
Related Videos
Related Practice