Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Introduction to Functions
Problem 2
Textbook Question
Express the radius of a sphere as a function of the sphere’s surface area. Then express the surface area as a function of the volume.
 Verified step by step guidance
Verified step by step guidance1
Start by recalling the formula for the surface area of a sphere, which is given by \( A = 4\pi r^2 \), where \( A \) is the surface area and \( r \) is the radius.
To express the radius \( r \) as a function of the surface area \( A \), solve the surface area formula for \( r \). Begin by dividing both sides by \( 4\pi \) to isolate \( r^2 \): \( r^2 = \frac{A}{4\pi} \).
Take the square root of both sides to solve for \( r \): \( r = \sqrt{\frac{A}{4\pi}} \). This expresses the radius as a function of the surface area.
Next, recall the formula for the volume of a sphere, which is \( V = \frac{4}{3}\pi r^3 \), where \( V \) is the volume.
To express the surface area \( A \) as a function of the volume \( V \), first solve the volume formula for \( r \): \( r = \left(\frac{3V}{4\pi}\right)^{1/3} \). Substitute this expression for \( r \) into the surface area formula \( A = 4\pi r^2 \) to express \( A \) in terms of \( V \).
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Surface Area of a Sphere
The surface area of a sphere is calculated using the formula A = 4πr², where A represents the surface area and r is the radius. This relationship shows how the surface area increases with the square of the radius, indicating that even small changes in radius can lead to significant changes in surface area.
Recommended video:
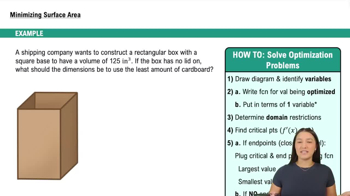
Example 1: Minimizing Surface Area
Volume of a Sphere
The volume of a sphere is given by the formula V = (4/3)πr³, where V is the volume and r is the radius. This formula illustrates that the volume grows with the cube of the radius, meaning that the volume increases much more rapidly than the surface area as the radius increases.
Recommended video:

Example 5: Packaging Design
Function Representation
In mathematics, expressing one quantity as a function of another involves defining a relationship where one variable depends on another. For example, expressing the radius as a function of surface area and then surface area as a function of volume requires rearranging the respective formulas to isolate the desired variable, demonstrating the interconnectedness of geometric properties.
Recommended video:

Properties of Functions

 1:36m
1:36mWatch next
Master Introduction to Calculus Channel with a bite sized video explanation from Callie
Start learning