Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals3h 25m
1. Limits and Continuity
Introduction to Limits
Problem 2.5.53a
Textbook Question
Complete the following steps for the given functions.
a. Find the slant asymptote of .
 Verified step by step guidance
Verified step by step guidance1
Perform polynomial long division of the numerator \(x^2 - 2x + 5\) by the denominator \(3x - 2\).
Divide the leading term of the numerator \(x^2\) by the leading term of the denominator \(3x\) to get the first term of the quotient, \(\frac{1}{3}x\).
Multiply the entire divisor \(3x - 2\) by \(\frac{1}{3}x\) and subtract the result from the original numerator \(x^2 - 2x + 5\).
Repeat the process with the new polynomial obtained after subtraction to find the next term of the quotient.
The slant asymptote is the linear part of the quotient obtained from the division, which is \(y = \frac{1}{3}x + \text{(constant)}\).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Slant Asymptote
A slant (or oblique) asymptote occurs when the degree of the numerator of a rational function is exactly one higher than the degree of the denominator. To find it, you perform polynomial long division on the function. The quotient (ignoring the remainder) gives the equation of the slant asymptote, which describes the behavior of the function as x approaches infinity or negative infinity.
Recommended video:

Introduction to Cotangent Graph
Polynomial Long Division
Polynomial long division is a method used to divide a polynomial by another polynomial of lower degree. It involves dividing the leading term of the numerator by the leading term of the denominator, multiplying the entire denominator by this result, and subtracting it from the numerator. This process is repeated until the degree of the remainder is less than that of the denominator, allowing us to find the slant asymptote.
Recommended video:

Introduction to Polynomial Functions
Rational Functions
Rational functions are expressions formed by the ratio of two polynomials. They can exhibit various behaviors, including vertical and horizontal asymptotes, depending on the degrees of the numerator and denominator. Understanding the properties of rational functions is crucial for analyzing their graphs and determining their asymptotic behavior, including the identification of slant asymptotes.
Recommended video:
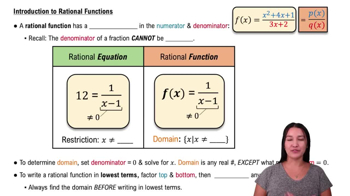
Intro to Rational Functions

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning