Find the domain of the rational function. Then, write it in lowest terms.f(x)=x2+9x−3f\left(x\right)=\frac{x^2+9}{x-3}f(x)=x−3x2+9

{x∣x≠3}, f ( x ) = x 2 + 9 x − 3 f\left(x\right)=\frac{x^2+9}{x-3} f ( x ) = x − 3 x 2 + 9

Find the domain of the rational function. Then, write it in lowest terms. f ( x ) = x 2 + 9 x − 3 f\left(x\right)=\frac{x^2+9}{x-3} f ( x ) = x − 3 x 2 + 9

Hey, everyone. Let's take a look at this practice problem. Here, we want to find the domain of the rational function and then write it in lowest terms. So let's go ahead and start by finding the domain. Now when we find the domain, we want to take our denominator and set it equal to 0. So here doing that, I can go ahead and solve for x by simply adding 3 to both sides. Now that will cancel over here, leaving me with x is equal to 3, and this represents my domain restriction. So I know that my domain is now x such that x cannot be equal to 3 because that would make my denominator 0. So this is our domain. Let's go ahead and write this in lowest terms. So taking another look at my function here, f of x is equal to x squared plus 9 divided by x minus 3. Remember, we want to fully factor both the top and the bottom of our fraction. But looking at the top here, x squared plus 9 is actually not going to factor any further. It's just going to remain x squared plus 9. Now our denominator also cannot be factored any further. It's just x minus 3. So this is actually actually already in lowest terms, x squared plus 9 divided by x minus 3. So I don't need to do anything. I don't need to cancel anything out with my function, and this is my function in lowest terms. Thanks for watching, and I'll see you in the next video.

Find the domain of the rational function. Then, write it in lowest terms. f ( x ) = x 2 + 9 x − 3 f\left(x\right)=\frac{x^2+9}{x-3} f ( x ) = x − 3 x 2 + 9

{x∣x≠3}, f ( x ) = x 2 + 9 x − 3 f\left(x\right)=\frac{x^2+9}{x-3} f ( x ) = x − 3 x 2 + 9

{x∣x≠0}, f ( x ) = 1 x − 3 f\left(x\right)=\frac{1}{x-3} f ( x ) = x − 3 1

{x∣x≠−3}, f ( x ) = x 2 + 9 x − 3 f\left(x\right)=\frac{x^2+9}{x-3} f ( x ) = x − 3 x 2 + 9

{x∣x≠3}, f ( x ) = x + 3 f\left(x\right)=x+3 f ( x ) = x + 3

0. Functions

Common Functions

Calculus

0. Functions

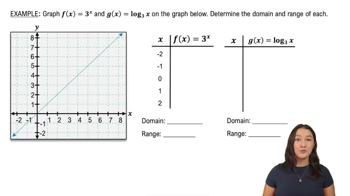
Common Functions

Struggling with Calculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

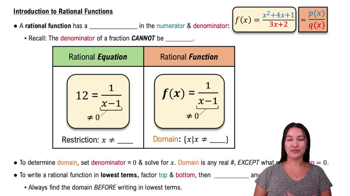
Find the domain of the rational function. Then, write it in lowest terms.
$f\left(x\right)=\frac{x^2+9}{x-3}$

{x∣x≠0}, $f\left(x\right)=\frac{1}{x-3}$

{x∣x≠3}, $f\left(x\right)=\frac{x^2+9}{x-3}$

{x∣x≠−3}, $f\left(x\right)=\frac{x^2+9}{x-3}$

{x∣x≠3}, $f\left(x\right)=x+3$

Verified step by step guidance

First, identify the rational function given: $ f(x) = \frac{x^2 + 9}{x - 3} $. A rational function is a fraction where both the numerator and the denominator are polynomials.

To find the domain of the function, determine the values of $ x $ that make the denominator zero, as these values are not allowed in the domain. Set the denominator equal to zero: $ x - 3 = 0 $. Solving this equation gives $ x = 3 $. Therefore, the domain of $ f(x) $ is all real numbers except $ x = 3 $, which can be written as $ \{ x \mid x \neq 3 \} $.

Next, simplify the rational function if possible. Check if the numerator $ x^2 + 9 $ can be factored or simplified in a way that might cancel with the denominator. In this case, $ x^2 + 9 $ does not factor in a way that cancels with $ x - 3 $, so the function remains $ f(x) = \frac{x^2 + 9}{x - 3} $.

Consider if there are any common factors between the numerator and the denominator. Since there are no common factors, the function is already in its lowest terms.

Finally, verify the simplified function and domain. The function $ f(x) = \frac{x^2 + 9}{x - 3} $ is in its lowest terms, and the domain is $ \{ x \mid x \neq 3 \} $.