Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals3h 25m
1. Limits and Continuity
Continuity
Problem 2.6.15
Textbook Question
What is the domain of f(x)=e^x/x and where is f continuous?
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the domain of the function.
Step 2: Recognize that the function f(x) = \frac{e^x}{x} is a rational function.
Step 3: Determine where the denominator is zero, since division by zero is undefined.
Step 4: Set the denominator x equal to zero and solve for x.
Step 5: Conclude that the domain of f(x) is all real numbers except x = 0, and f is continuous on its domain.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain of a Function
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. For the function f(x) = e^x/x, we need to identify values of x that do not lead to undefined expressions, such as division by zero. In this case, the function is undefined at x = 0, so the domain is all real numbers except zero.
Recommended video:
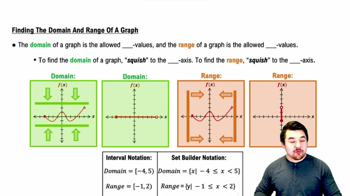
Finding the Domain and Range of a Graph
Continuity of a Function
A function is continuous at a point if the limit of the function as it approaches that point equals the function's value at that point. For f(x) = e^x/x, we must check continuity at all points in its domain. Since the function is undefined at x = 0, it is not continuous there, but it is continuous for all other real numbers.
Recommended video:

Intro to Continuity
Exponential Functions
Exponential functions, such as e^x, are characterized by a constant base raised to a variable exponent. They are defined for all real numbers and exhibit rapid growth. In the context of f(x) = e^x/x, the exponential component contributes to the function's behavior as x approaches positive or negative infinity, influencing its overall continuity and limits.
Recommended video:

Exponential Functions
Related Videos
Related Practice