Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
Continuity
Problem 1c
Textbook Question
Textbook QuestionWhich of the following functions are continuous for all values in their domain? Justify your answers.
c. T(t)=temperature t minutes after midnight in Chicago on January 1
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
1mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
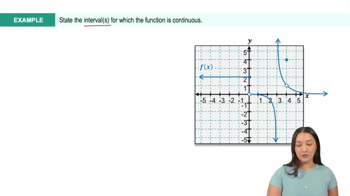
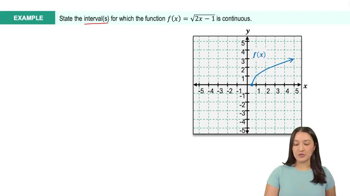
Continuity of Functions
A function is continuous at a point if the limit of the function as it approaches that point equals the function's value at that point. For a function to be continuous over its entire domain, it must be continuous at every point in that domain. This means there are no breaks, jumps, or asymptotes in the function's graph.
Recommended video:

Intro to Continuity
Domain of a Function
The domain of a function is the set of all possible input values (or 't' values) for which the function is defined. Understanding the domain is crucial for determining continuity, as a function may be continuous on its domain but not defined outside of it. For example, a temperature function may only be defined for certain time intervals.
Recommended video:
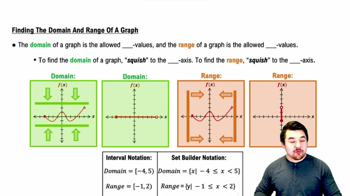
Finding the Domain and Range of a Graph
Real-World Context of Functions
In applied mathematics, functions often represent real-world phenomena, such as temperature over time. Analyzing these functions requires understanding how they behave in practical scenarios. For instance, temperature changes throughout the day can be modeled as a continuous function, but external factors may introduce discontinuities that need to be considered.
Recommended video:

Real World Application
Related Videos
Related Practice