Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
4. Applications of Derivatives
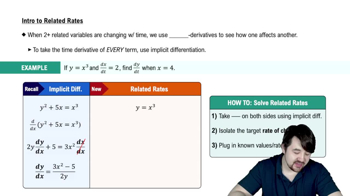
Related Rates
Problem 3.7.104b
Textbook Question
{Use of Tech} A mixing tank A 500-liter (L) tank is filled with pure water. At time t=0, a salt solution begins flowing into the tank at a rate of 5 L/min. At the same time, the (fully mixed) solution flows out of the tank at a rate of 5.5 L/min. The mass of salt in grams in the tank at any time t≥0 is given by M(t) = 250(1000−t)(1−10−³⁰(1000−t)¹⁰) and the volume of solution in the tank is given by V(t) = 500-0.5t.
b. Graph the volume function and verify that the tank is empty when t=1000 min.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the volume function V(t) = 500 - 0.5t, which represents the volume of the solution in the tank at any time t. The initial volume is 500 L, and it decreases by 0.5 L per minute due to the outflow rate being higher than the inflow rate.
Step 2: To graph the volume function V(t), identify key points. Start with the initial condition at t = 0, where V(0) = 500 L. Then, find the volume at other significant times, such as t = 1000 min.
Step 3: Calculate V(1000) to verify when the tank is empty. Substitute t = 1000 into the volume function: V(1000) = 500 - 0.5(1000). Simplify this expression to find the volume at t = 1000.
Step 4: Plot the graph of V(t) using the points calculated. The graph should be a straight line with a negative slope, starting at (0, 500) and ending at (1000, 0).
Step 5: Verify that the tank is empty at t = 1000 by confirming that V(1000) = 0. This confirms that the volume function correctly models the situation where the tank is empty at 1000 minutes.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Related Videos
Related Practice