Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Transformations
Problem 40d
Textbook Question
Textbook QuestionThe graph of ƒ is shown in the figure. Graph the following functions. <IMAGE>
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
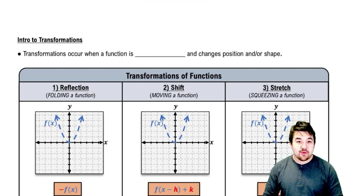
Function Transformation
Function transformation refers to the changes made to the graph of a function based on modifications to its equation. Common transformations include vertical and horizontal shifts, stretches, and reflections. For example, the expression f(2(x - 1)) indicates a horizontal shift to the right by 1 unit and a horizontal compression by a factor of 2.
Recommended video:
Intro to Transformations
Horizontal Stretch and Compression
Horizontal stretch and compression involve altering the width of the graph of a function. A factor greater than 1 compresses the graph, making it narrower, while a factor between 0 and 1 stretches it, making it wider. In the function f(2(x - 1)), the '2' compresses the graph horizontally, affecting how quickly the function values change as x varies.
Recommended video:

Intro to Transformations
Graphing Composite Functions
Graphing composite functions involves plotting the output of one function as the input to another. In this case, f(2(x - 1)) means we first apply the transformation to x, then evaluate the function f at that transformed value. Understanding how to graph composite functions is essential for visualizing the effects of transformations on the original function's graph.
Recommended video:

Evaluate Composite Functions - Special Cases

 5:25m
5:25mWatch next
Master Intro to Transformations with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice

