Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
Introduction to Limits
Problem 2.2.29
Textbook Question
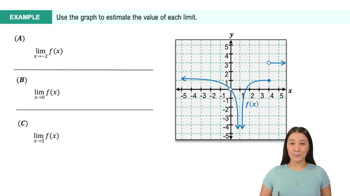
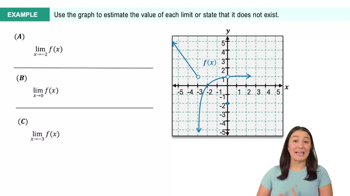
Use a graph of f to estimate or to show that the limit does not exist. Evaluate f(x) near to support your conjecture.
 Verified step by step guidance
Verified step by step guidance1
Identify the function given: \( f(x) = \frac{1 - \cos(2x - 2)}{(x - 1)^2} \) and the point \( a = 1 \).
Recognize that the limit \( \lim_{x \to 1} f(x) \) involves a \( \frac{0}{0} \) indeterminate form, as both the numerator and denominator approach zero when \( x = 1 \).
Apply L'Hôpital's Rule, which is used to evaluate limits of indeterminate forms \( \frac{0}{0} \) or \( \frac{\infty}{\infty} \), by differentiating the numerator and the denominator separately.
Differentiate the numerator: \( \frac{d}{dx}[1 - \cos(2x - 2)] = 2\sin(2x - 2) \).
Differentiate the denominator: \( \frac{d}{dx}[(x - 1)^2] = 2(x - 1) \).
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Limit of a Function
The limit of a function describes the behavior of the function as the input approaches a certain value. It is denoted as lim(x→a) f(x) and indicates what value f(x) approaches as x gets closer to a. Understanding limits is crucial for analyzing continuity and differentiability, as well as for evaluating functions that may not be defined at certain points.
Recommended video:

Limits of Rational Functions: Denominator = 0
Continuity
A function is continuous at a point if the limit of the function as it approaches that point equals the function's value at that point. For the function f(x) to be continuous at x = a, it must satisfy three conditions: f(a) must be defined, the limit as x approaches a must exist, and both must be equal. Discontinuities can lead to limits that do not exist or are undefined.
Recommended video:

Intro to Continuity
Graphical Interpretation of Limits
Using a graph to estimate limits involves observing the behavior of the function as it approaches a specific x-value. By analyzing the graph, one can identify trends, such as whether the function approaches a finite value, diverges, or oscillates. This visual approach aids in understanding the concept of limits and can provide insights into the existence or non-existence of limits at certain points.
Recommended video:

Finding Limits Numerically and Graphically

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning