Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
2. Intro to Derivatives
Tangent Lines and Derivatives
Problem 10
Textbook Question
If f′(−2) = 7, find an equation of the line tangent to the graph of f at the point (−2,4).
 Verified step by step guidance
Verified step by step guidance1
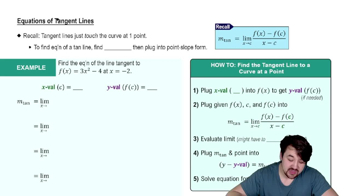
Step 1: Recall that the equation of a line in point-slope form is given by y - y_1 = m(x - x_1), where m is the slope and (x_1, y_1) is a point on the line.
Step 2: Identify the slope of the tangent line. Since f'(-2) = 7, the slope of the tangent line at x = -2 is 7.
Step 3: Identify the point on the graph where the tangent line touches. The problem states that the point is (-2, 4).
Step 4: Substitute the slope (m = 7) and the point (-2, 4) into the point-slope form equation: y - 4 = 7(x + 2).
Step 5: Simplify the equation if needed to express it in a different form, such as slope-intercept form (y = mx + b), by distributing and rearranging terms.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Derivative
The derivative of a function at a given point represents the slope of the tangent line to the graph of the function at that point. In this case, f′(−2) = 7 indicates that the slope of the tangent line at x = -2 is 7.
Recommended video:

Derivatives
Point-Slope Form
The point-slope form of a linear equation is given by y - y₁ = m(x - x₁), where (x₁, y₁) is a point on the line and m is the slope. This form is particularly useful for writing the equation of a tangent line when a point and slope are known.
Recommended video:
Guided course
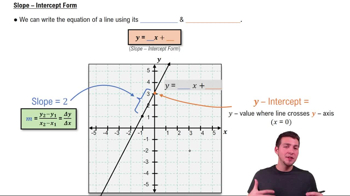
Slope-Intercept Form
Tangent Line
A tangent line to a curve at a given point is a straight line that touches the curve at that point without crossing it. The equation of the tangent line can be derived using the slope from the derivative and the coordinates of the point on the curve.
Recommended video:
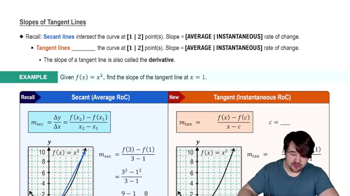
Slopes of Tangent Lines

 5:13m
5:13mWatch next
Master Slopes of Tangent Lines with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice