Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
Introduction to Limits
Problem 2.5.63a
Textbook Question
Textbook QuestionDetermine whether the following statements are true and give an explanation or counterexample.
a. The graph of a function can never cross one of its horizontal asymptotes.
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Horizontal Asymptotes
A horizontal asymptote is a line that a graph approaches as the input values (x) approach positive or negative infinity. It indicates the behavior of a function at extreme values. For example, the function f(x) = 1/x has a horizontal asymptote at y = 0, meaning as x becomes very large or very small, the function values get closer to 0.
Recommended video:
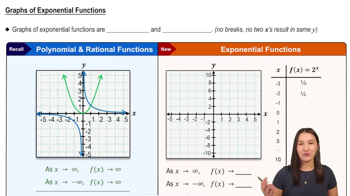
Graphs of Exponential Functions
Behavior of Functions Near Asymptotes
Functions can behave differently near their asymptotes. While a function may approach a horizontal asymptote, it is not restricted from crossing it at finite values of x. For instance, the function f(x) = sin(x)/x approaches the horizontal asymptote y = 0 as x approaches infinity, but it crosses the x-axis multiple times.
Recommended video:

Graphs of Exponential Functions
True/False Statements in Mathematics
In mathematics, determining the truth of a statement often requires understanding definitions and properties. A statement can be true in some contexts and false in others. In this case, the assertion that a function cannot cross its horizontal asymptote is false, as demonstrated by functions that do cross their asymptotes at finite points.
Recommended video:

Solving Exponential Equations Using Like Bases

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning