Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
3. Techniques of Differentiation
Product and Quotient Rules
Problem 3.4.17
Textbook Question
Find the slope of the line tangent to the graph of f(x) = x / x+6 at the point (3, 1/3) and at (-2, -1/2).
 Verified step by step guidance
Verified step by step guidance1
Step 1: To find the slope of the tangent line to the graph of a function at a given point, we need to find the derivative of the function, f(x). The function given is f(x) = \frac{x}{x+6}.
Step 2: Use the quotient rule to differentiate f(x). The quotient rule states that if you have a function h(x) = \frac{u(x)}{v(x)}, then h'(x) = \frac{u'(x)v(x) - u(x)v'(x)}{(v(x))^2}. Here, u(x) = x and v(x) = x + 6.
Step 3: Calculate the derivatives u'(x) and v'(x). For u(x) = x, u'(x) = 1. For v(x) = x + 6, v'(x) = 1.
Step 4: Substitute u(x), v(x), u'(x), and v'(x) into the quotient rule formula to find f'(x). This will give you the expression for the derivative of f(x).
Step 5: Evaluate f'(x) at the given points (3, 1/3) and (-2, -1/2) to find the slopes of the tangent lines at these points. Substitute x = 3 and x = -2 into the expression for f'(x) to find the respective slopes.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
5mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Derivative
The derivative of a function at a given point represents the slope of the tangent line to the graph of the function at that point. It is calculated as the limit of the average rate of change of the function as the interval approaches zero. In this context, finding the derivative of f(x) = x / (x + 6) will allow us to determine the slope at specific points.
Recommended video:

Derivatives
Tangent Line
A tangent line to a curve at a given point is a straight line that touches the curve at that point without crossing it. The slope of the tangent line is equal to the derivative of the function at that point. In this problem, we need to find the slope of the tangent line at the points (3, 1/3) and (-2, -1/2) by evaluating the derivative of the function at these x-values.
Recommended video:
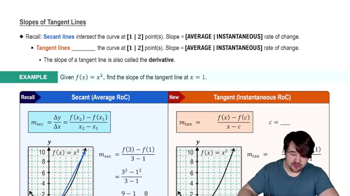
Slopes of Tangent Lines
Point-Slope Form
The point-slope form of a linear equation is used to express the equation of a line given a point on the line and its slope. It is written as y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope. This form is useful for constructing the equation of the tangent line once the slope has been determined from the derivative.
Recommended video:
Guided course
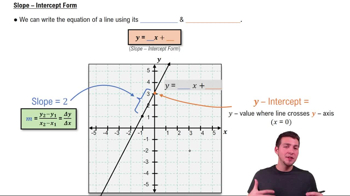
Slope-Intercept Form
Related Videos
Related Practice










