Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
Continuity
Problem 1d
Textbook Question
Which of the following functions are continuous for all values in their domain? Justify your answers.
d. p(t)=number of points scored by a basketball player after t minutes of a basketball game
 Verified step by step guidance
Verified step by step guidance1
<p>1. **Understand the Function**: The function \( p(t) \) represents the number of points scored by a basketball player after \( t \) minutes of a game. This is a real-world scenario where the function is defined in terms of time and points scored.</p>
<p>2. **Identify the Nature of the Function**: In this context, \( p(t) \) is a step function. A step function is a piecewise constant function that jumps from one value to another without taking on intermediate values. In a basketball game, points are scored in discrete amounts (e.g., 2 points for a field goal, 3 points for a three-pointer), and the score changes instantaneously at the moment a basket is made.</p>
<p>3. **Determine Continuity**: A function is continuous if there are no breaks, jumps, or holes in its graph. For \( p(t) \), since it is a step function, it will have jumps at the moments when points are scored. Therefore, \( p(t) \) is not continuous because it has discontinuities at the times when the player scores.</p>
<p>4. **Consider the Domain**: The domain of \( p(t) \) is the duration of the basketball game, typically from \( t = 0 \) to the end of the game. Within this domain, the function is defined, but it is not continuous due to the nature of scoring in discrete steps.</p>
<p>5. **Conclusion**: Conclude that \( p(t) \) is not continuous for all values in its domain because it is a step function with jumps at the points where the player scores.</p>
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Continuity of Functions
A function is continuous at a point if the limit of the function as it approaches that point equals the function's value at that point. For a function to be continuous over its entire domain, it must be continuous at every point in that domain. This means there are no breaks, jumps, or asymptotes in the function's graph.
Recommended video:

Intro to Continuity
Domain of a Function
The domain of a function is the set of all possible input values (x-values) for which the function is defined. Understanding the domain is crucial for determining continuity, as a function may be continuous within its domain but not defined outside of it. For example, a function that involves division cannot include values that make the denominator zero.
Recommended video:
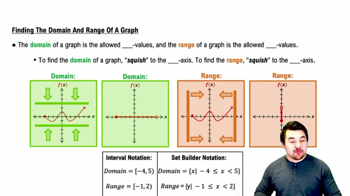
Finding the Domain and Range of a Graph
Real-World Applications of Functions
In real-world scenarios, such as the scoring of a basketball player over time, functions can model behaviors that are inherently continuous. For instance, the number of points scored can be represented as a function of time, where the function is continuous as long as points are scored in a consistent manner without sudden jumps, reflecting the natural flow of the game.
Recommended video:

Real World Application
Related Videos
Related Practice