Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 2h 22m
0. Functions
Introduction to Functions
Problem 1.20
Textbook Question
In Exercises 19–32, find the (a) domain and (b) range.
____
𝔂 = -2 + √1 - x
 Verified step by step guidance
Verified step by step guidance1
Step 1: Identify the expression inside the square root, which is '1 - x'. The square root function is defined only for non-negative values, so set up the inequality 1 - x ≥ 0.
Step 2: Solve the inequality 1 - x ≥ 0 to find the domain of the function. Rearrange the inequality to find the values of x that satisfy it.
Step 3: The domain of the function is the set of x-values for which the expression inside the square root is non-negative. Express this domain in interval notation.
Step 4: To find the range, consider the values that the expression √(1 - x) can take. Since the square root function outputs non-negative values, determine the minimum and maximum values of √(1 - x).
Step 5: The range of the function is determined by the expression -2 + √(1 - x). Calculate the minimum and maximum values of this expression based on the domain found in Step 3, and express the range in interval notation.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Domain of a Function
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. For the function y = -2 + √(1 - x), the expression under the square root must be non-negative, which imposes restrictions on x. Thus, determining the domain involves solving the inequality 1 - x ≥ 0.
Recommended video:
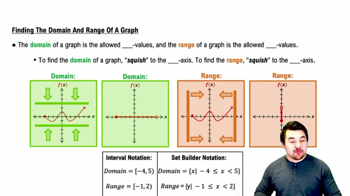
Finding the Domain and Range of a Graph
Range of a Function
The range of a function is the set of all possible output values (y-values) that the function can produce. For the function y = -2 + √(1 - x), the square root function outputs non-negative values, which means the minimum value of y occurs when x is at its maximum in the domain. Analyzing the function helps identify the range based on the values y can take.
Recommended video:

Finding the Domain and Range of a Graph
Square Root Function
The square root function, denoted as √x, is defined for non-negative values of x and produces non-negative outputs. In the context of the function y = -2 + √(1 - x), the square root affects both the domain and range, as it restricts x to values where 1 - x is non-negative, and it shifts the output down by 2, impacting the overall range.
Recommended video:

Multiplying & Dividing Functions

 1:36m
1:36mWatch next
Master Introduction to Calculus Channel with a bite sized video explanation from Callie
Start learning