Determine if the function f ( x ) f\left(x\right) f ( x ) is continuous and/or differentiable at x = 3 x=3 x = 3 .

in this problem, we're asked to determine if the function f of x is continuous and or differentiable at x equals 3. Now to solve this problem, the first thing I'm going to do is check whether or not the function is continuous, because that should always be your first step when solving these types of problems. Now the way that I'm going to do this is by taking the left side of this equation, which would be for when x is less than 3, and setting it equal to the right side of this equation at our value of interest x equals 3. So we're going to have x squared, which should be 3 squared, and that's going to be equal 2 times x or 2 times 3 plus 3. Now 3 squared is 9, 2 times 3 is 6, and 6 plus 3 is 9. So this function is continuous since both sides of the equation will equal each other if we set them equal to our points of interest where we replace the this value of 3 in for x. But now we need to figure out if it's differentiable. So we have that it's continuous. And to figure out whether or not it's differentiable, well, we need to use this same strategy of setting the left and right side equal to each other or seeing if they're equal. But the way that we need to do this is by finding the derivatives and seeing if those are equal at the value of 3. Now, since we're looking for a specific point of interest, I'm going to use this version of the equation. So we're going to have f prime of c, that's going to be the limit as x approaches c for f of x minus f of c all divided by x minus c. This is the equation for the derivative at a certain point. Now I'm first going to check for the left side of our of our piecewise function here. So we're going to have that f prime, our point of interest is 3, are going to have the limit as x approaches 3, and then we're going to have our function x squared minus 3 squared all divided by x minus 3. That's using this equation. Now what I can see here is that I can't just take 3 and plug it in for x because 3 minus 3 is 0. We cannot divide by 0, but what I can do is try to factor or simplify the top in some sort of way. Now x squared minus 3 squared, that's a difference of squares. So this can actually be factored to be x plus 3 times x minus 3, and all of this is going to be divided by x minus 3. Now at this point, the x minus threes will cancel, and from here I can take this value of 3 and plug it in for x. So, we're going to have 3 plus 3 which is equal to 6, and I was able to do that since this x minus 3 cancelled, meaning we no longer have an error if we put this value of 3 for x, so we ended up getting 6. So that means from the left side, we're going to get 6. But, what about from the right side? Well to figure this out, we need to take the derivative of the right side at an x value of 3. So we're going to have f prime of 3, and this time we're going to use the right side function of the piece here, which is going to be 2x plus 3, and that's going to be minus f of c, which would be 2 times 3 plus 3, this whole thing, and that's all going to be divided by x minus 3. And don't forget for this whole function that we have right here, there's a limit attached to this fraction. That's going to be the limit as x approaches our value of interest, which in this case is 3. Now from here, what I can do is try to simplify the top, because again, I can't take this 3 and plug it in here. That's gonna be dividing by a 0, 3 minus 3, but I can try to simplify the top. So we'll have 2x plus 3, and again, we have this limit still attached. You wanna keep this limit on. And then we'll have 2x plus 3, and then we're going to have minus and then 2 times 3. Now 2 times 3 is 6, so we're going to have minus 6, and then we'll distribute this negative sign over there, so we're going to have minus 3. And then this is all gonna be divided by x minus 3. Now at this point, what I can do is cancel the positive 3 with the negative 3 there. So what we're going to end up having is we'll keep this limit attached. We'll have a limit as x approaches 3, and then it's going to be 2x minus 6 over x minus 3. Now I can take this 2 and I can actually factor it out of the top. So we're going to have the limit as x approaches 3, and that's going to be 2 times x minus 3 over x minus 3, in which case these x minus threes are going to cancel. So all we're going to be left with is 2, and we don't even have to worry about the limit because 2 is just a constant right there. So, what that means is for the right side of this equation we end up getting a value of 2. But notice that 6 clearly does not equal 2. So, what does that mean? Well, we we can see that it is continuous, but when we use the derivatives, we can see that it is not differentiable. So the solution to this problem would be that it's continuous but not differentiable, and that's the answer to this problem that we have. So that is how you can solve the situations where you have these piecewise functions and need to determine whether or not it's continuous and or differentiable. So hope you found this video helpful, and let's go ahead and get some more practice.

2. Intro to Derivatives

Differentiability

Calculus

2. Intro to Derivatives

Differentiability

Struggling with Calculus?

Join thousands of students who trust us to help them ace their exams!

Multiple Choice

Determine if the function $f\left(x\right)$ is continuous and/or differentiable at $x=3$ .

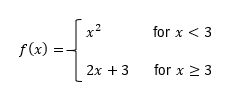
Continuous and non-differentiable

Continuous and differentiable

Discontinuous and non-differentiable

Discontinuous and differentiable

Verified step by step guidance

To determine if the function is continuous at x=3, check if the left-hand limit, right-hand limit, and the function value at x=3 are equal. Calculate the left-hand limit as x approaches 3 from the left using f(x) = x^2.

Calculate the right-hand limit as x approaches 3 from the right using f(x) = 2x + 3.

Evaluate the function at x=3 using the definition for x >= 3, which is f(x) = 2x + 3.

If the left-hand limit, right-hand limit, and the function value at x=3 are all equal, the function is continuous at x=3.

To determine differentiability at x=3, check if the derivative from the left and the derivative from the right are equal. Calculate the derivative of f(x) = x^2 for x < 3 and f(x) = 2x + 3 for x >= 3, and compare their values at x=3.

5:02m

Watch next

Master Determining Differentiability Graphically with a bite sized video explanation from Patrick

Differentiability practice set

Problem sets built by lead tutors

Expert video explanations

Struggling with Calculus?

Determine if the functionf(x)f\left(x\right)f(x) is continuous and/or differentiable at x=3x=3x=3.

Watch next

Differentiability practice set

Determine if the function $f\left(x\right)$ is continuous and/or differentiable at $x=3$ .