Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
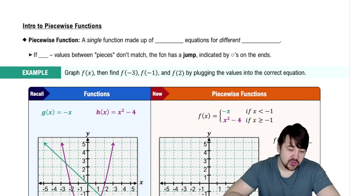
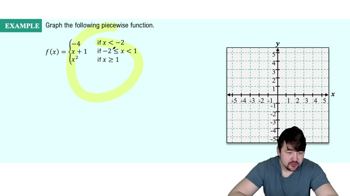
Piecewise Functions
Problem 49c
Textbook Question
Textbook QuestionArea functions Let A(x) be the area of the region bounded by the t -axis and the graph of y=ƒ(t) from t=0 to t=x. Consider the following functions and graphs.
c. Find a formula for A(x)
ƒ(t) =6 <IMAGE>
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Definite Integral
The definite integral of a function over an interval gives the net area under the curve of that function between two points. In this context, to find the area function A(x), we use the definite integral of the function f(t) from 0 to x, which mathematically is expressed as A(x) = ∫[0 to x] f(t) dt. This concept is fundamental in calculus as it connects the geometric interpretation of area with the analytical process of integration.
Recommended video:

Introduction to Indefinite Integrals
Area Under a Curve
The area under a curve represents the total space between the curve and the x-axis over a specified interval. For the function f(t), the area A(x) from t=0 to t=x quantifies how much space is enclosed by the graph of f(t) and the t-axis. Understanding this concept is crucial for solving problems related to area functions, as it directly relates to the application of integration.
Recommended video:
Summary of Curve Sketching Example 2
Function Notation
Function notation, such as A(x) or f(t), is a way to represent mathematical functions and their outputs. In this case, A(x) denotes the area as a function of x, while f(t) represents the function whose area we are calculating. Grasping function notation is essential for interpreting and manipulating mathematical expressions correctly, especially in calculus where functions are frequently analyzed and transformed.
Recommended video:

Multiplying & Dividing Functions
Related Videos
Related Practice