Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals3h 25m
1. Limits and Continuity
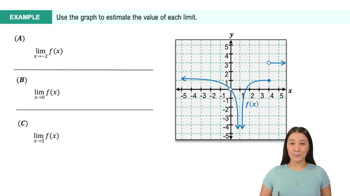
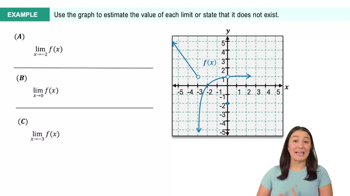
Introduction to Limits
Problem 2.7.21
Textbook Question
Use the precise definition of a limit to prove the following limits. Specify a relationship between ε and δ that guarantees the limit exists.
lim x→4 x^2−16 / x−4=8 (Hint: Factor and simplify.)
 Verified step by step guidance
Verified step by step guidance1
Step 1: Recognize that the expression \( \frac{x^2 - 16}{x - 4} \) is undefined at \( x = 4 \). To simplify, factor the numerator: \( x^2 - 16 = (x - 4)(x + 4) \).
Step 2: Simplify the expression by canceling the common factor \( x - 4 \) in the numerator and denominator, resulting in \( x + 4 \) for \( x \neq 4 \).
Step 3: According to the definition of a limit, for every \( \varepsilon > 0 \), there must exist a \( \delta > 0 \) such that if \( 0 < |x - 4| < \delta \), then \( \left| \frac{x^2 - 16}{x - 4} - 8 \right| < \varepsilon \).
Step 4: Substitute the simplified expression into the limit condition: \( \left| (x + 4) - 8 \right| = |x - 4| \).
Step 5: To satisfy the limit condition, choose \( \delta = \varepsilon \). This ensures that whenever \( 0 < |x - 4| < \delta \), \( |x - 4| < \varepsilon \), proving the limit exists and equals 8.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
2mPlay a video:
Was this helpful?

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning