Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
0. Functions
Common Functions
Problem 19.
Textbook Question
Textbook QuestionEvaluating trigonometric functions Without using a calculator, evaluate the following expressions or state that the quantity is undefined.
cos (2π/3)
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
3mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Unit Circle
The unit circle is a circle with a radius of one centered at the origin of a coordinate plane. It is fundamental in trigonometry as it allows for the definition of sine, cosine, and tangent functions based on the coordinates of points on the circle. For any angle θ, the x-coordinate corresponds to cos(θ) and the y-coordinate corresponds to sin(θ).
Recommended video:
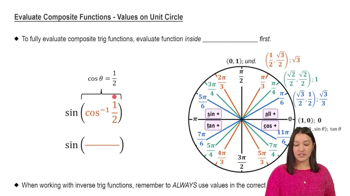
Evaluate Composite Functions - Values on Unit Circle
Reference Angles
Reference angles are the acute angles formed by the terminal side of an angle and the x-axis. They help in evaluating trigonometric functions for angles greater than 90 degrees or less than 0 degrees by relating them to their corresponding acute angles. For example, the reference angle for 2π/3 is π/3, which is used to find the cosine value.
Recommended video:
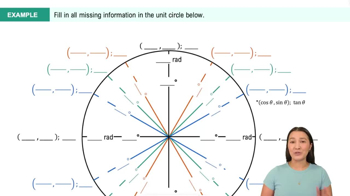
Trig Values in Quadrants II, III, & IV Example 2
Cosine Function
The cosine function, denoted as cos(θ), represents the x-coordinate of a point on the unit circle corresponding to the angle θ. It is periodic with a period of 2π and has specific values for common angles. For instance, cos(π/3) equals 1/2, and since 2π/3 is in the second quadrant, where cosine is negative, cos(2π/3) equals -1/2.
Recommended video:

Graph of Sine and Cosine Function

 5:57m
5:57mWatch next
Master Graphs of Common Functions with a bite sized video explanation from Nick
Start learningRelated Videos
Related Practice