Table of contents
- 0. Functions7h 52m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms34m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
1. Limits and Continuity
Introduction to Limits
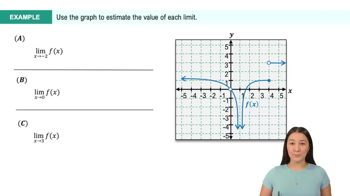
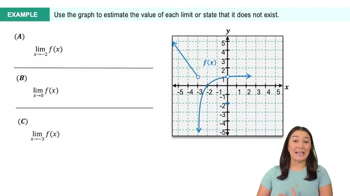
Problem 2.5.61
Textbook Question
Determine the end behavior of the following transcendental functions by analyzing appropriate limits. Then provide a simple sketch of the associated graph, showing asymptotes if they exist.
 Verified step by step guidance
Verified step by step guidance1
Step 1: Understand the function f(x) = sin(x). The sine function is periodic with a period of 2π, meaning it repeats its values every 2π units along the x-axis.
Step 2: Analyze the range of the sine function. The sine function oscillates between -1 and 1 for all x, so its range is [-1, 1].
Step 3: Determine the end behavior by considering the limits as x approaches positive and negative infinity. Since sin(x) is periodic and bounded, it does not approach a specific value as x approaches infinity or negative infinity.
Step 4: Identify any asymptotes. The sine function does not have any vertical or horizontal asymptotes because it is bounded and periodic.
Step 5: Sketch the graph of f(x) = sin(x). Draw a wave-like pattern oscillating between -1 and 1, repeating every 2π along the x-axis, with no asymptotes.
Recommended similar problem, with video answer:
 Verified Solution
Verified SolutionThis video solution was recommended by our tutors as helpful for the problem above
Video duration:
12mPlay a video:
Was this helpful?

 6:47m
6:47mWatch next
Master Finding Limits Numerically and Graphically with a bite sized video explanation from Callie
Start learning