For the following graph, find the open intervals for which the function is concave up or concave down. Identify any inflection points.

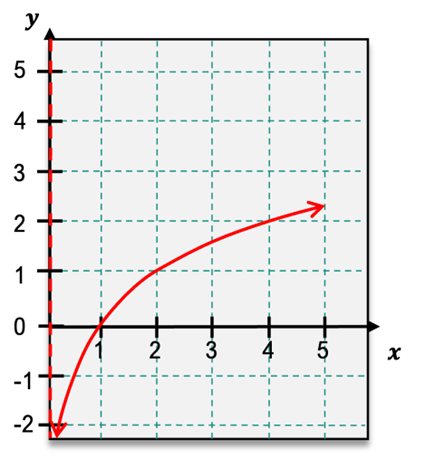
• A. Concave down: $\left(0,\infty\right)$; No inflection pt
• B. Concave down: $\left(0,\infty\right)$; Inflection pt: $\left(0,0\right)$
• C. Concave up: $\left(-\infty,0\right)$; Concave down: $\left(0,\infty\right)$; Inflection pt: $\left(0,0\right)$
• D. Concave down: $\left(-\infty,\infty\right)$; No inflection pt